【統計学の応用】単回帰分析

回帰分析の有用性

統計学やデータ分析において、回帰分析は極めて重要な手法です。

この分析手法は、ある変数（従属変数）が他の変数（独立変数）にどのように影響を受けるかを理解するために使用されます。

特に単回帰分析は、独立変数が1つだけのシンプルなモデルであり、予測や関係性の理解において基礎的な役割を果たします。この方法を用いることで、現実のデータから数値的な関係を導き出し、未来の予測や戦略立案に応用することが可能となります。

単回帰分析

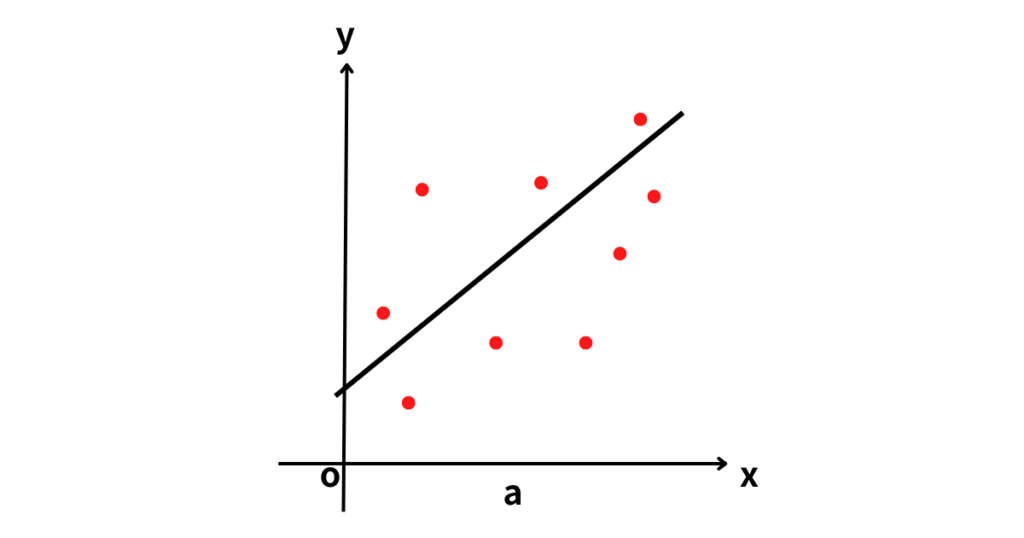
母回帰直線

単回帰分析における基本的な概念として「母回帰直線」があります。母回帰直線とは、母集団全体での独立変数と従属変数の間の関係を表す直線です。これは理論上のモデルであり、データが従うべき理想的な直線関係を示します。この直線は、以下のような式で表されます。

　\(Y=\beta_0+\beta_1X\)

ここで、\(Y\) は従属変数、\(X\) は独立変数、\(\beta_0\) は切片（直線が \(Y\) 軸と交わる点）、\(\beta_1\) は回帰係数（独立変数の増加に伴う従属変数の変化量）です。

実際のデータでは、すべての点がこの直線上に乗るわけではなく、誤差項が生じます。この誤差項は、実際のデータが母回帰直線からどれだけ離れているかを示し、分析の精度に影響を与えます。

最小二乗法

次に、単回帰分析で重要な手法として「最小二乗法」が挙げられます。最小二乗法は、データポイントと回帰直線の間の距離（誤差）の二乗和を最小化することで、最も適した回帰直線を求める方法です。具体的には、以下の数式で表されるものを最小化します。

　\(\text{誤差の二乗和} = \sum_{i=1}^{n} (Y_i – (\beta_0 + \beta_1X_i))^2\)

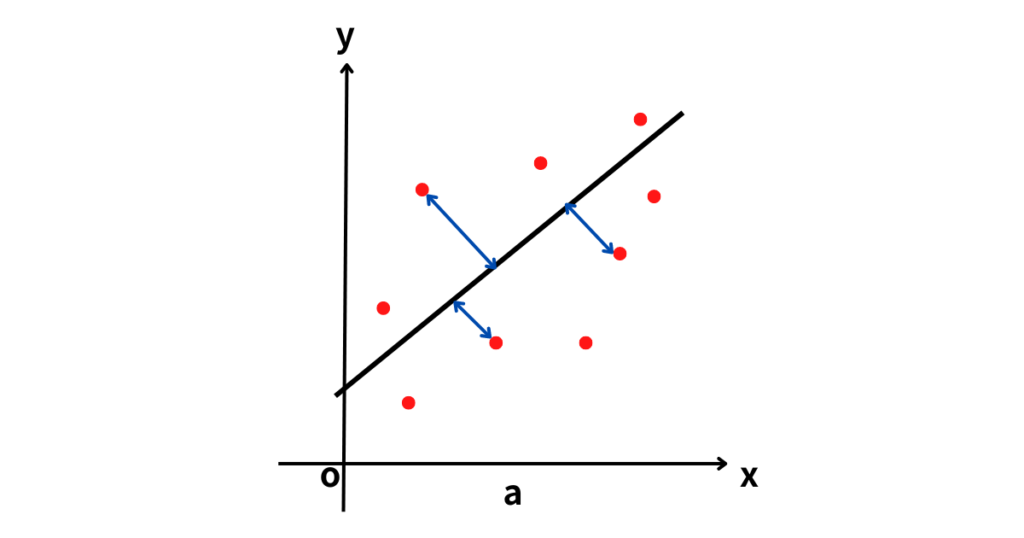
この式では、\(Y_i\) は各データポイントの実際の値、\(X_i\) は対応する独立変数の値、\(\beta_0\) と \(\beta_1\) は直線の切片と傾きです。この二乗和を最小にすることで、データに最も合致する回帰直線が得られます。最小二乗法は、回帰分析の精度と信頼性を高めるために不可欠な手法です。

偏回帰係数

単回帰分析において、偏回帰係数は非常に重要な役割を果たします。偏回帰係数とは、他の独立変数が一定のとき、1つの独立変数が従属変数に与える影響の大きさを表します。単回帰分析では、独立変数が1つしかないため、偏回帰係数はそのまま回帰係数として扱われます。

回帰係数が正であれば、独立変数が増加するにつれて従属変数も増加することを意味し、負であれば独立変数が増加するにつれて従属変数が減少することを意味します。この係数は、データに基づいて算出され、将来の予測や因果関係の解釈において重要な指標となります。

回帰分析を使って変数間の関係を理解する例として、以下のようなシンプルなシナリオを考えてみましょう。

単回帰分析の例

評価：決定係数

単回帰分析の結果を評価する際、決定係数（\(R^2\)）が用いられます。決定係数は、回帰モデルがどれだけデータを説明できているかを示す指標で、\(0\) から \(1\) までの値を取ります。1に近いほど、モデルがデータをよく説明できていることを意味し、0に近いほど説明力が低いことを意味します。

決定係数は、以下のように計算されます。

　\(R^2 = 1 – \frac{\sum_{i=1}^{n} (Y_i – \hat{Y}i)^2}{\sum{i=1}^{n} (Y_i – \bar{Y})^2}\)

ここで、\(Y_i\) は実際のデータポイント、\(\hat{Y}_i\) は回帰モデルによる予測値、\(\bar{Y}\) は従属変数の平均値です。決定係数が高い場合、モデルはデータをよく説明していると解釈されます。

単回帰分析のまとめ

単回帰分析は、データの関係性を理解し、予測を行うための基本的かつ強力な手法です。

母回帰直線、最小二乗法、偏回帰係数、決定係数といった概念を理解することで、単回帰分析の基礎をしっかりと押さえることができます。

これらの概念を基に、より複雑な回帰分析やデータ解析手法に進むことが可能です。単回帰分析を適切に用いることで、ビジネスや研究において有益な洞察を得ることができるでしょう。