ベクトルと平行四辺形
今回はベクトルの成分表示および平行四辺形の頂点に関する問題です!
始点の変換方法(分割)
\(\overrightarrow{PQ}=\bigcirc\overrightarrow{Q}-\bigcirc\overrightarrow{P}\)
ベクトルの大きさ
\(\overrightarrow{a}=(a_1\), \(a_2)\) のとき、\(|\overrightarrow{a}|=\sqrt{a_1^2+a_2^2}\)
平行四辺形 \(ABCD\) の特徴
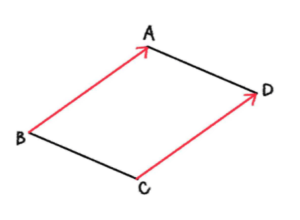
辺 \(BA\) と辺 \(CD\) について、長さが等しいかつ平行なので、\(\overrightarrow{BA}=\overrightarrow{CD}\)
平行四辺形(問題)
\(3\) 点 \(A(1,\) \(3)\), \(B(3,\), \(-2)\), \(C(4\), \(1)\) がある。
(1) \(\overrightarrow{AB}\), \(\overrightarrow{BC}\), \(\overrightarrow{CA}\) の成分と大きさをそれぞれ求めよ。
(2) 四角形 \(ABCD\) が平行四辺形であるとき、点 \(D\) の座標を求めよ。
(3) (2) の平行四辺形について、\(2\) 本の対角線の長さを求めよ。
>>詳細はこちらから
解説
(1) \(\overrightarrow{OA}=(1,\ 3)\), \(\overrightarrow{OB}=(3,\ -2)\), \(\overrightarrow{OC}=(4,\ 1)\) と表せるので、
始点の変換方法(分割)
\(\overrightarrow{PQ}=\bigcirc\overrightarrow{Q}-\bigcirc\overrightarrow{P}\)
\(\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(3-1,\ -2-3)=(2,\ -5)\)
\(\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=(4-3,\ 1+2)=(1,\ 3)\)
\(\overrightarrow{CA}=\overrightarrow{OA}-\overrightarrow{OC}=(1-4,\ 3-1)=(-3,\ 2)\)
ベクトルの大きさ
\(\overrightarrow{a}=(a_1\), \(a_2)\) のとき、\(|\overrightarrow{a}|=\sqrt{a_1^2+a_2^2}\)
\(|\overrightarrow{AB}|=\sqrt{2^2+(-5)^2}=\sqrt{29}\)
\(|\overrightarrow{BC}|=\sqrt{1^2+3^2}=\sqrt{10}\)
\(|\overrightarrow{CA}|=\sqrt{(-3)^2+2^2}=\sqrt{13}\)
(2) 四角形 \(ABCD\) が平行四辺形であるとき、点 \(D\) の座標を求めよ。
四角形 \(ABCD\) は平行四辺形であり、辺 \(AB\) と 辺 \(DC\) は長さが同じで平行なので、\(\overrightarrow{AB}=\overrightarrow{BC}\)
よって、\((2,\ -5)=(4-a,\ 1-b)\)
ゆえに、\(2=4-a\), \(-5=1-b\)
これを解いて、\(a=2\), \(b=6\) したがって、\(D(2,\ 6)\)
(3) (2) の平行四辺形について、\(2\) 本の対角線の長さを求めよ。
\(2\) 本の対角線の長さは \(|\overrightarrow{AC}|\), \(|\overrightarrow{BD}|\) である。
よって、(1) から \(|\overrightarrow{AC}|=\sqrt{13}\)
\(\overrightarrow{BD}=\overrightarrow{OD}-\overrightarrow{OB}=(2-3,\ 6+2)=(-1,\ 8)\)
\(|\overrightarrow{BD}|=\sqrt{(-1)^2+8^2}=\sqrt{65}\)
おわりに
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている学生の方
- 公務員試験の数学で困っている学生/社会人の方
- 統計学(統計検定)の勉強で困っている学生/社会人の方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
時間や料金などは相談して決められればと思っておりますが、塾に通うよりは高コスパかなと思います。また、基本的にはオンラインでの授業を想定していますが、場所によっては直接の指導が可能です。(プロフィール)
これまでは塾講師や高校で働いていたのですが、現在はデータサイエンティストとして活動しています。社会やビジネスで数学がどのように使われているのか、そういった話も交えながら進められればと思っております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。





質問や感想はコメントへ!