今回は、三角形の角の大きさと辺の長さの関係について説明します。
三角形の形状を大雑把に分類すると次の3つに分けられます。
・鋭角三角形
・直角三角形
・鈍角三角形
上記の分類は、
(コサイン) \(>0\) のとき、\(0^{\circ}\) から \(90^{\circ}\)
(コサイン) \(<0\) のとき、\(90^{\circ}\) から \(180^{\circ}\)
という余弦（コサイン）の性質により分類することができます。
三角形の辺と角の大小関係
三角形について、次のことが成り立つことが知られています。
三角形の2辺の大小関係は、その向かい合う核の大小関係と一致する。
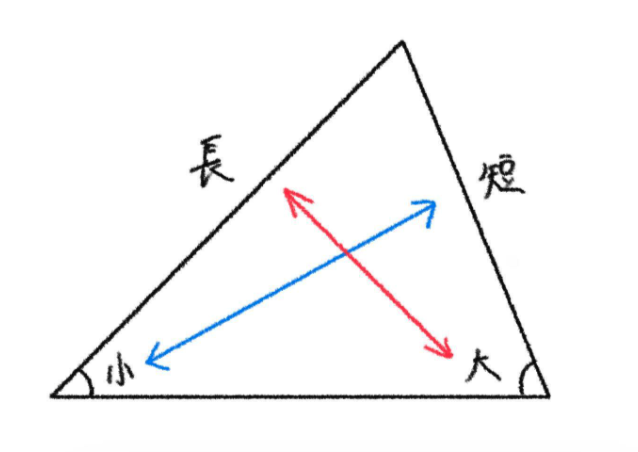
つまり、辺が大きければ大きいほど向かい合う角は大きくなるし、辺が小さければ小さいほど向かい合う角は小さくなる。
（証明）
次のような直線 \(AB\) と直線 \(AB\) 上の点 \(Q\) を考える。
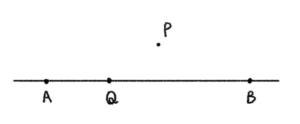
直線 \(AB\) 上に点 \(Q\) をとり、\(\angle{PQB}\) を考える。点 \(P\) から直線 \(AB\) に下ろした垂線の足を \(H\) とすると、\(H\) より \(A\) 側に点 \(Q\) があるとき、\(\angle{PQB}\) は鋭角になり、線分 \(BH\) 上に点 \(Q\) があるときは \(\angle{PQB}\) は鈍角になる。
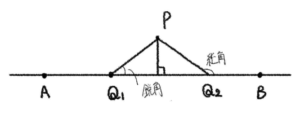
この結果から、点 \(Q\) を \(A\) から \(B\) の方へ動かすにつれて、\(\angle{PQB}\) は大きくなることが分かる。
まず、\(AC>BC\) である \(\triangle{ABC}\) について、\(A<B\) であることを証明する。\(BC=CD\) となるように辺 \(AC\) 上に点 \(D\) をとると、\(\triangle{BCD}\) は二等辺三角形であるから、\(\angle{CDB}=\angle{CBD}\) となる。
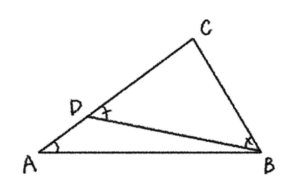
ここで、\(\angle{BAC}<\angle{BDC}\) であるから、\(\angle{BAC}<\angle{CBD}\)、すなわち \(A<B\) である。逆に \(A<B\) のときも同様に考えれば \(AC>BC\) であることは明らかである。したがって、三角形の \(2\) 辺の大小関係は、その向かい合う角の大小関係と一致する。
＞＞詳細はこちらから
三角形の形状を調べる方法
直角三角形・鋭角三角形・鈍角三角形のいずれかであるかを調べる方法を説明します。
三角形の内角の和は \(180^{\circ}\) であるから、三角形の3つの辺のうち、最も長い辺の体格が最大角であり、それ以外の2つの角は必ず鋭角である。
【三角形の形状を調べる方法】
三角形の内角の1つに着目したとき、その角が鋭角・直角・鈍角かを調べるには、その角のコサインの符号を調べれば良い。例えば、\(A\) を調べるときは、余弦定理を利用して
\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)
の符号を調べれば良い。ここで、分母の \(2bc\) は常に正であるから、\(\cos A\) の符号と \(b^2+c^2-a^2\) の符号は一致する。つまり、\(b^2+c^2-a^2\) の符号を調べれば良いことになる。ちなみにこれは \(a^2\) と \(b^2+c^2\) の大小関係を調べることと同じである。
① \(a^2<b^2+c^2\) のとき、鋭角三角形
② \(a^2=b^2+c^2\) のとき、直角三角形
③ \(a^2>b^2+c^2\) のとき、鈍角三角形
三角形の形状を調べる問題
問題
\(\triangle{ABC}\) において、3辺の長さが次のようなとき、\(\triangle{ABC}\) は鋭角三角形、直角三角形、鈍角三角形のいずれかであるか。
(1) \(a=4\), \(b=3\), \(c=2\)
(2) \(a=5\), \(b=6\), \(c=7\)
(3) \(a=12\), \(b=13\), \(c=5\)
【(1) の解説】
最大辺の長さが \(a=4\) であるから、
\(a^2=4^2=16\)
\(b^2+c^2=3^2+2^2=13\)
となるから、\(a^2>b^2+c^2\) である。
よって、\(\triangle{ABC}\) は鈍角三角形である。
【(2) の解説】
最大辺の長さが \(c=7\) であるから、\(c^2\) と \(a^2+b^2\) の大小関係を調べる。
\(c^2=7^2=49\)
\(a^2+b^2=5^2+6^2=61\)
となるから、\(c^2<a^2+b^2\) である。
よって、\(\triangle{ABC}\) は鋭角三角形である。
【(3) の解説】
最大辺の長さが \(b=13\) であるから、\(b^2\) と \(c^2+a^2\) の大小関係を調べる。
\(b^2=13^2=169\)
\(c^2+a^2=12^2+5^2=169\)
となるから、\(b^2=c^2+a^2\) である。
よって、\(\triangle{ABC}\) は直角三角形である。
おわりに
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！