【図形の性質】チェバの定理とその覚え方

URLをコピーしました！

チェバの定理

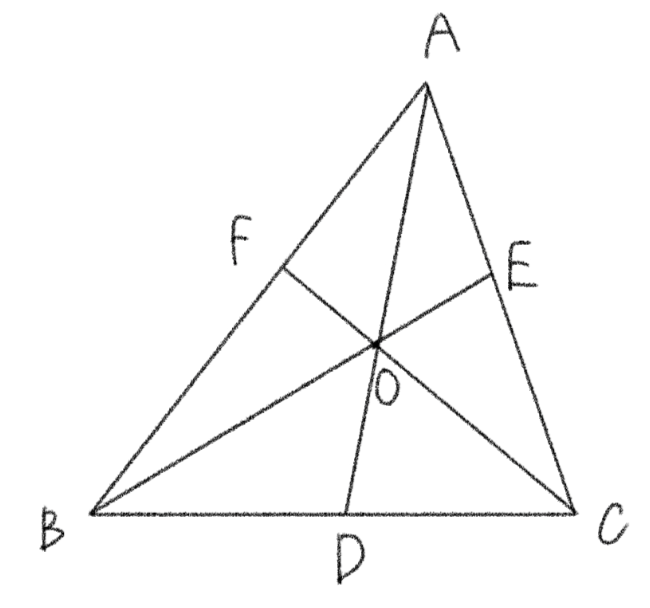
三角形 $ABC$ において、任意の点 $O$ をとり、直線 $AO$ と $BC$、$BO$ と $CA$、$CO $と $AB$ の交点をそれぞれ $D$、$E$、$F$ とする。この時、次の等式が成立する。なお、点 $O$は、三角形の内部にあっても外部にあってもよい。

　$$\displaystyle\frac{AF}{FB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}=1$$

↓メネラウスの定理についてはこちら

【図形の性質】メネラウスの定理とその覚え方

チェバの定理の覚え方

① 図の頂点の流れで覚える。
② 定理の日本語をセットで覚える。
　※片方だけでなく両方を意識して覚えると良いです。①だけ覚えてる方が多いですが、それだけだと形が少し変わっただけで対応できなくなるので両方覚えておくのがおすすめです。

① 図の頂点の流れで覚える。

下の図のように、点 $A$ をスタート地点とし、そこから分数の分子 → 分母の順番で反時計回りに繋がっていくように定理を作っていきます。

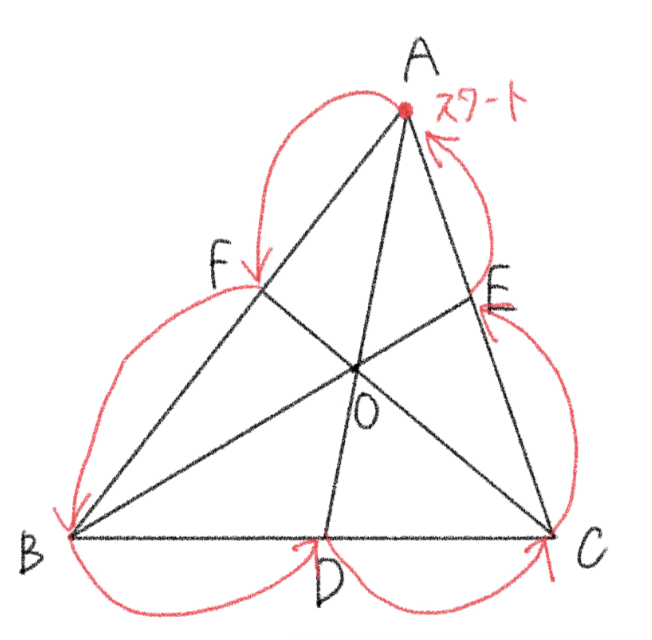
$$\displaystyle\frac{AF}{FB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}=1$$

② 定理の日本語をセットで覚える。

日本語で覚えておくことにより図の形が変わっても対応することができます。

　「三角形 $ABC$において、任意の点 $O$ をとり」を簡単な言葉で言い換えると、「三角形 $ABC$ を描いて、どこでもいいので点をうつ。」となります。

よって、点 $O$ は以下のように三角形 $ABC$ の外部にあっても良いわけです。

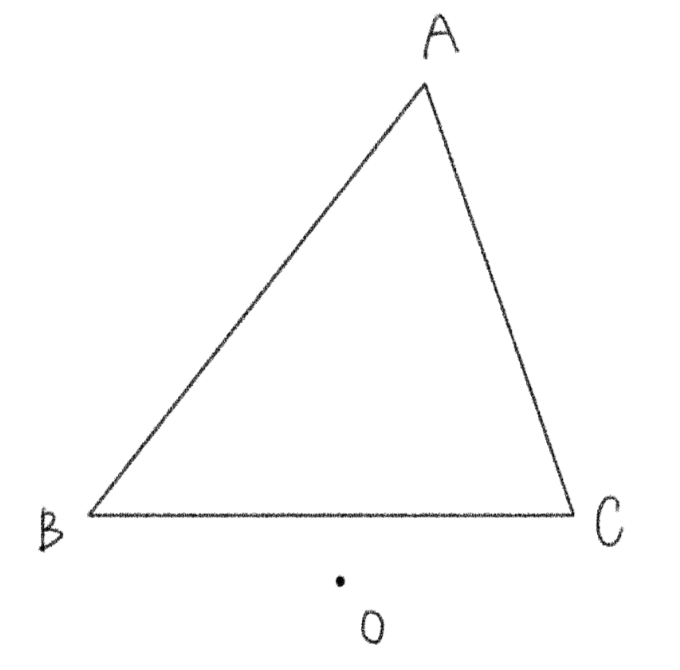
その場合、図は以下のようになります。

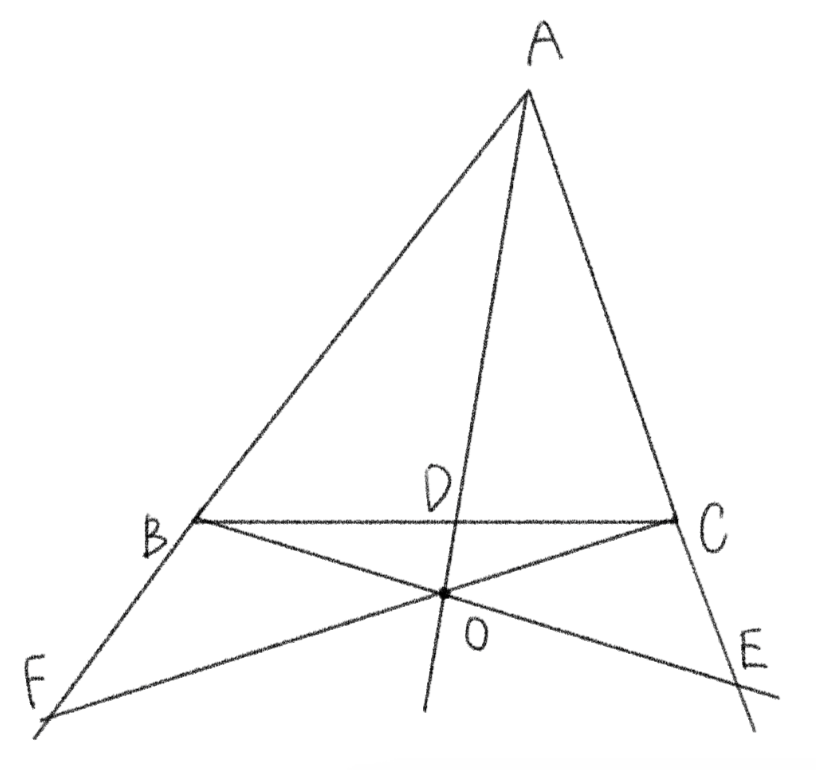
このような図でも得られる式は先ほどと同様の式になります。

$$\displaystyle\frac{AF}{FB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}=1$$

チェバの定理の証明

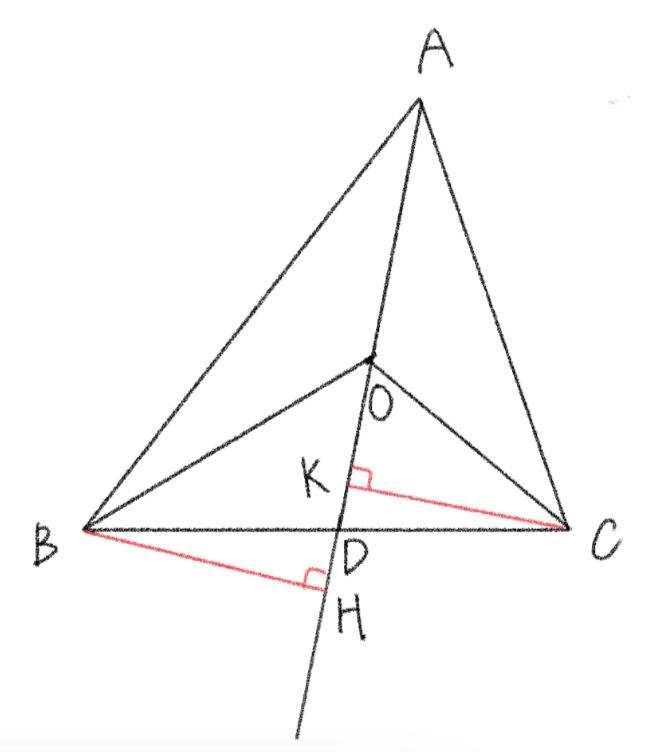
　上の図のように、底辺 $OA$ を共有する $\triangle{OAB}$,　$\triangle{OAC}$ があり、直線 $OA$,　$BC$ が点 $D$ で交わるとする。また、$2$ 点 $B$,　$C$ から直線 $OA$ に下ろした垂線をそれぞれ $BH$,　$CK$ とすると、線分 $BH$ と $CK$ は平行なので、

$\triangle{CKD}\sim\triangle{BHD}$ より
※$\sim$：相似の記号

　$BH:CK=BD:CD$

　$BH\cdot CD=BD\cdot CK$

　$\displaystyle\frac{BH}{CK}=\frac{BD}{DC}$　($CD=DC$)$\cdots$ ①

ここで、$\triangle{OAB}$ と $\triangle{OAC}$ は辺 $OA$ を共通の底辺としていることから、

　$\triangle{OAB}:\triangle{OAC}=BH:CK$

　$\triangle{OAC}\cdot BH=\triangle{OAB}\cdot CK$

　$\displaystyle\frac{\triangle{OAB}}{\triangle{OAC}}=\frac{BH}{CK}$ $\cdots$ ②

となり、①、② より

　$\displaystyle\frac{\triangle{OAB}}{\triangle{OAC}}=\frac{BD}{DC}$ $\cdots$ ③

同様に考えると、

　$\displaystyle\frac{\triangle{OBC}}{\triangle{OAB}}=\frac{CE}{EA}$$\cdots$ ④

　$\displaystyle\frac{\triangle{OCA}}{\triangle{OBC}}=\frac{AF}{FB}$$\cdots$ ⑤

④、⑤、⑥ の辺々を掛けると、

　$\displaystyle\frac{BD}{DC}\cdot\frac{CE}{EA}\cdot\frac{AF}{FB}$

$=\displaystyle\frac{\triangle{OAB}}{\triangle{OAC}}\cdot\frac{\triangle{OBC}}{\triangle{OAB}}\cdot \frac{\triangle{OCA}}{\triangle{OBC}}=1$$\cdots$ ⑤

よって、

　$\displaystyle\frac{BD}{DC}\cdot\frac{CE}{EA}\cdot\frac{AF}{FB}=1$

チェバの定理の問題

$1$ 辺の長さが $7$ の三角形 $ABC$ がある。辺 $AD$、$AC$ 上に $AD=3$、 $AE=6$ となるように $2$ 点 $D$、$E$ をとる。このとき、$BE$、$CD$ の交点を $F$、直線 $AF$、$BC$ との交点を $G$ とする。線分 $CG$ の長さを求めよ。

＞＞詳細はこちらから

（解説）

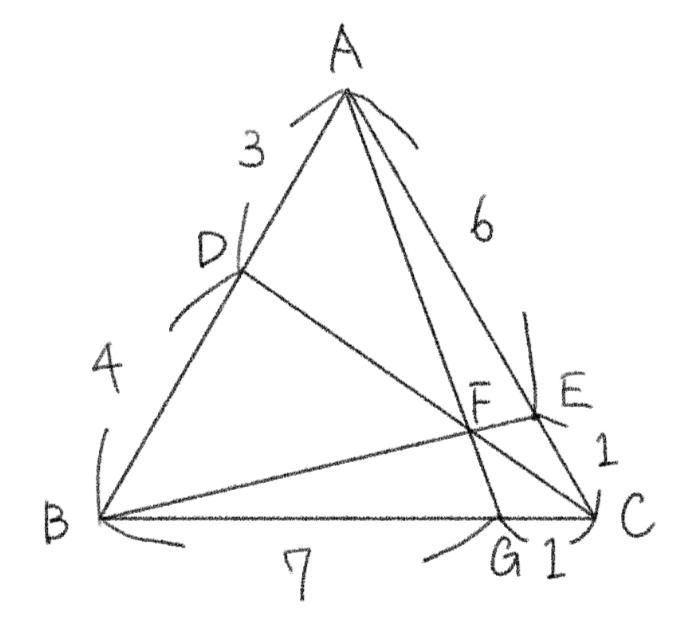
$AD=3$,　$DB=7-3=4$,　$AE=6$,　$CE=7-6=1$

チェバの定理より

　$\displaystyle\frac{AD}{DB}\cdot\frac{BG}{GC}\cdot\frac{CE}{EA}=1$

ゆえに、

　$\displaystyle\frac{3}{4}\cdot\frac{BG}{GC}\cdot\frac{1}{6}=1$

よって、

　$BG=8GC$

したがって、

　$CG:BG=1:8$

このことにより、

　$CG=BC\cdot\displaystyle\frac{1}{1+8}=\frac{7}{9}$

おわりに

さいごまで読んでいただきありがとうございました！

大学受験数学で困っている方
公務員試験の数学で困っている方
統計学（統計検定）の勉強で困っている方

個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）

私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。

周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。

だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。

数学に困っている方の一助になれれば幸いです。

ご連絡お待ちしております。

URLをコピーしました！

【図形の性質】チェバの定理とその覚え方

【図形の性質】方べきの定理