平均変化率とは、ある点とある点の通る傾きのこと
微分係数とは、ある点における接線の傾きを求めること

平均変化率と微分係数
平均変化率
平均変化率とは、ある点とある点の通る傾きのこと
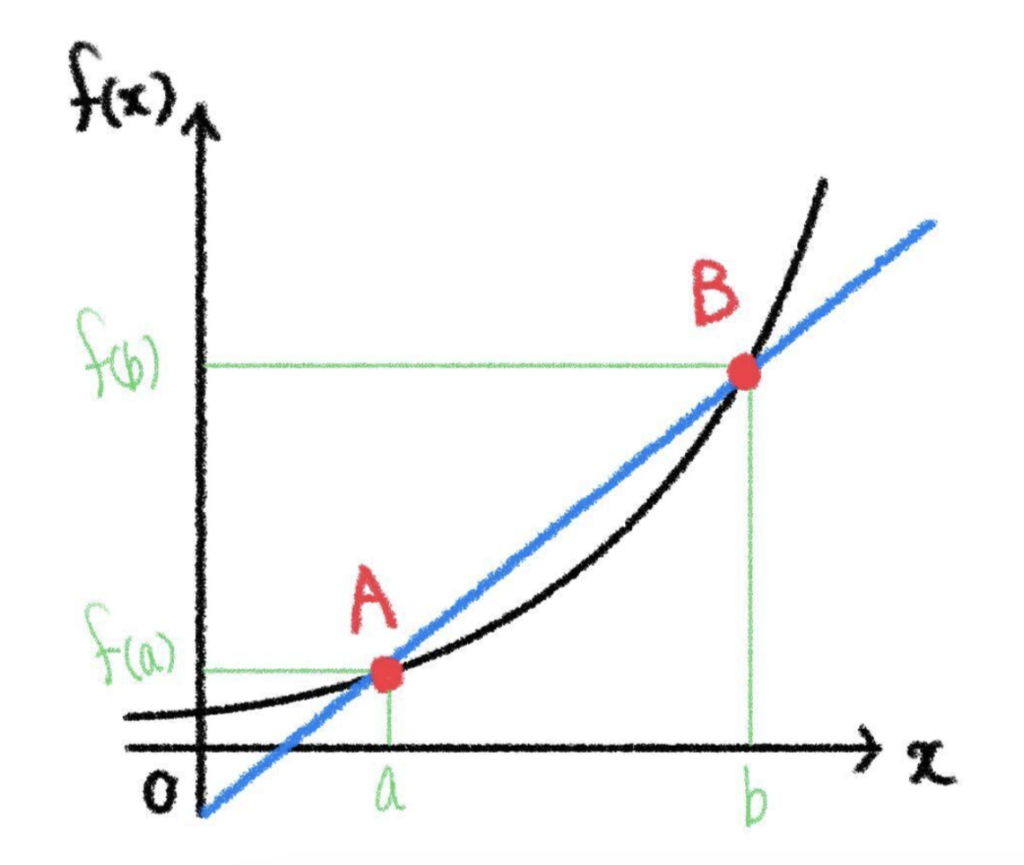
つまり、図において線分 \(AB\) の傾きを考えると、点 \(A\) から 点 \(B\) までの平均変化率になります。
\(\displaystyle\frac{f(b)-f(a)}{b-a}\)
微分係数
微分係数とは、ある点における接線の傾きを求めること
上記の図において、点 \(A\) における接線の傾きを求めるためには、点 \(B\) を 点 \(A\) に近づけていくと良いです。
\(\displaystyle\lim_{b \to a}\frac{f(b)-f(a)}{b-a}\)
また、\(b-a=h\) とおいて以下のようにも表されます。
\(\displaystyle\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}\)
例題
\(f(x)=x^2-x\) について、次のものを求めよ。
(1) \(x=1\) から \(x=1+h\) \((h\neq 0)\) まで変化するときの平均変化率
(2) \(x=1\) における微分係数
(3) 曲線 \(y=f(x)\) 上の点 \(A\) \((t\), \(f(t))\) における接戦の傾きが \(-1\) となるとき、\(t\) の値を求めよ。
解説
(1)
\(x=1\) のとき、\(f(1)=0\)
\(x=1+h\) のとき、\(f(1+h)=h^2+h\)
よって、
\(\displaystyle\frac{f(1+h)-f(1)}{(1+h)-1}\)
\(=\displaystyle\frac{h^2+h-0}{h}\)
\(=h+1\)
(2)
\(\displaystyle\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}\)
\(\displaystyle\lim_{h \to 0}\frac{f(1+h)-f(1)}{(1+h)-1}\)
\(=\displaystyle\lim_{h \to 0}\frac{h^2+h-0}{h}\)
\(=\displaystyle\lim_{h\to 0}(h+1)=1\)
(3)
\(\displaystyle\lim_{h \to 0}\frac{f(t+h)-f(t)}{h}=-1\) となるような \(t\) を求める。
左辺は、\(f(x)\) を微分して、\(x=t\) を代入した式なので、
\(f'(x)=2x-1\)
となり、 \(x=t\) を代入すると、
\(f'(t)=2t-1\)
したがって、
\(2t-1=-1\)
\(t=0\)
おわりに
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている学生の方
- 公務員試験の数学で困っている学生/社会人の方
- 統計学(統計検定)の勉強で困っている学生/社会人の方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
時間や料金などは相談して決められればと思っておりますが、塾に通うよりは高コスパかなと思います。また、基本的にはオンラインでの授業を想定していますが、場所によっては直接の指導が可能です。(プロフィール)
これまでは塾講師や高校で働いていたのですが、現在はデータサイエンティストとして活動しています。社会やビジネスで数学がどのように使われているのか、そういった話も交えながら進められればと思っております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。




質問や感想はコメントへ!