三次関数/四次関数の最大・最小
今回は三次関数や四次関数の最大・最小問題です!
基本的には、二次関数の最大・最小を求めるときの流れと同様にして解いていきます。
つまり、「グラフを描いて、\(y\) 軸の高低で最大・最小を求める」です。
”グラフを描く”の部分が二次関数とは違い、微分法を用います。
では、例題を見ていきましょう!
関数の最大・最小(問題)
次の関数の最大値と最小値を求めよ。また、そのときの \(x\) の値を求めよ。
(1) \(y=x^3-6x^2+10\) \((-2\leq x\leq 3)\)
(2) \(y=3x^4-4x^3-12x^2\) \((-1\leq x\leq 3)\)
>>詳細はこちらから
解説
(1) \(y=x^3-6x^2+10\) \((-2\leq x\leq 3)\)
\(y’=3x^2-12x\)
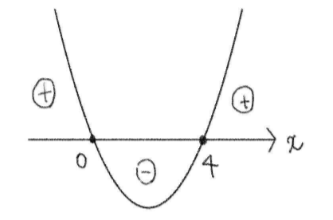
\(y’=0\) とおくと、
\(3x^2-12x=0\)
\(3x(x-4)=0\)
\(x=0\), \(4\)
上記のグラフを見ながら増減表を書くと、
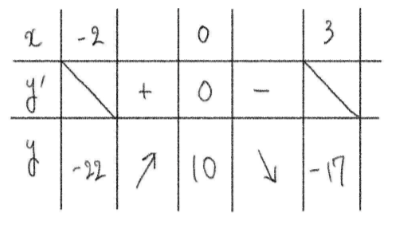
増減表より、
\(x=0\) のとき最大値 \(10\)
\(x=4\) のとき最小値 \(-22\)
(2) \(y=3x^4-4x^3-12x^2\) \((-1\leq x\leq 3)\)
\(y’=12x^3-12x^2-24x\)
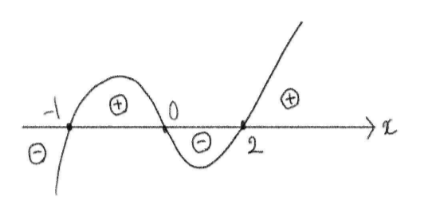
\(y’=0\) とおくと、
\(12x^3-12x^2-24x=0\)
\(12x(x^2-x-2)=0\)
\(12x(x-2)(x+1)=0\)
\(x=-1\), \(0\), \(2\)
上記のグラフを見ながら増減表を書くと、
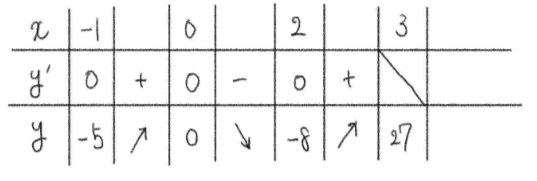
増減表より、
\(x=3\) のとき最大値 \(27\)
\(x=2\) のとき最小値 \(-8\)
おわりに
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている学生の方
- 公務員試験の数学で困っている学生/社会人の方
- 統計学(統計検定)の勉強で困っている学生/社会人の方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
時間や料金などは相談して決められればと思っておりますが、塾に通うよりは高コスパかなと思います。また、基本的にはオンラインでの授業を想定していますが、場所によっては直接の指導が可能です。(プロフィール)
これまでは塾講師や高校で働いていたのですが、現在はデータサイエンティストとして活動しています。社会やビジネスで数学がどのように使われているのか、そういった話も交えながら進められればと思っております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。





質問や感想はコメントへ!