関数の値の変化、最大・最小
関数の増加と減少
関数 \(f(x)\) が閉区間 \([a\), \(b]\) で連続で、開区間 \((a\), \(b)\) で微分可能であるとする。
1 開区間 \((a\), \(b)\) で常に \(f'(x)>0\) ならば、\(f(x)\) は \([a\), \(b]\) で単調に増加する
2 開区間 \((a\), \(b)\) で常に \(f'(x)<0\) ならば、\(f(x)\) は \([a\), \(b]\) で単調に減少する
3 開区間 \((a\), \(b)\) で常に \(f'(x)=0\) ならば、\(f(x)\) は \([a\), \(b]\) で定数である
上の説明と下の図の色がリンクしてるよ！
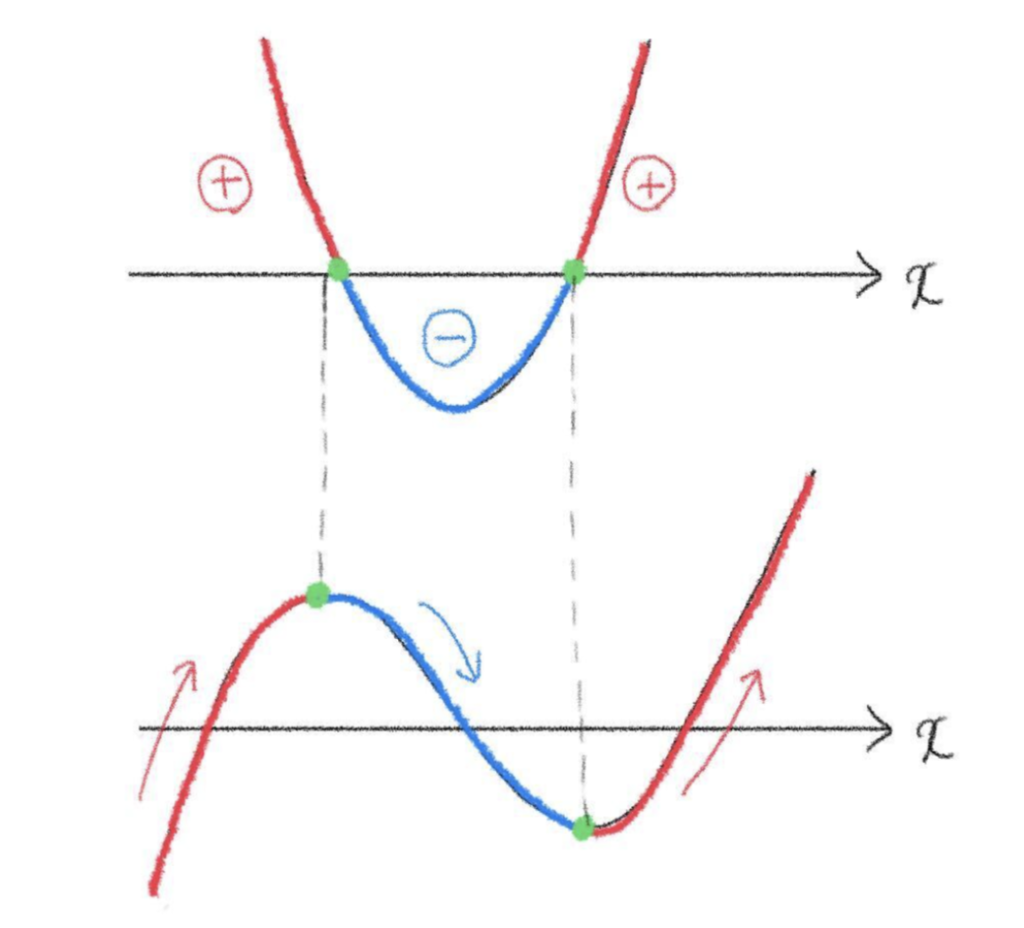
極大値と極小値の求め方
\(y=f(x)\) において、
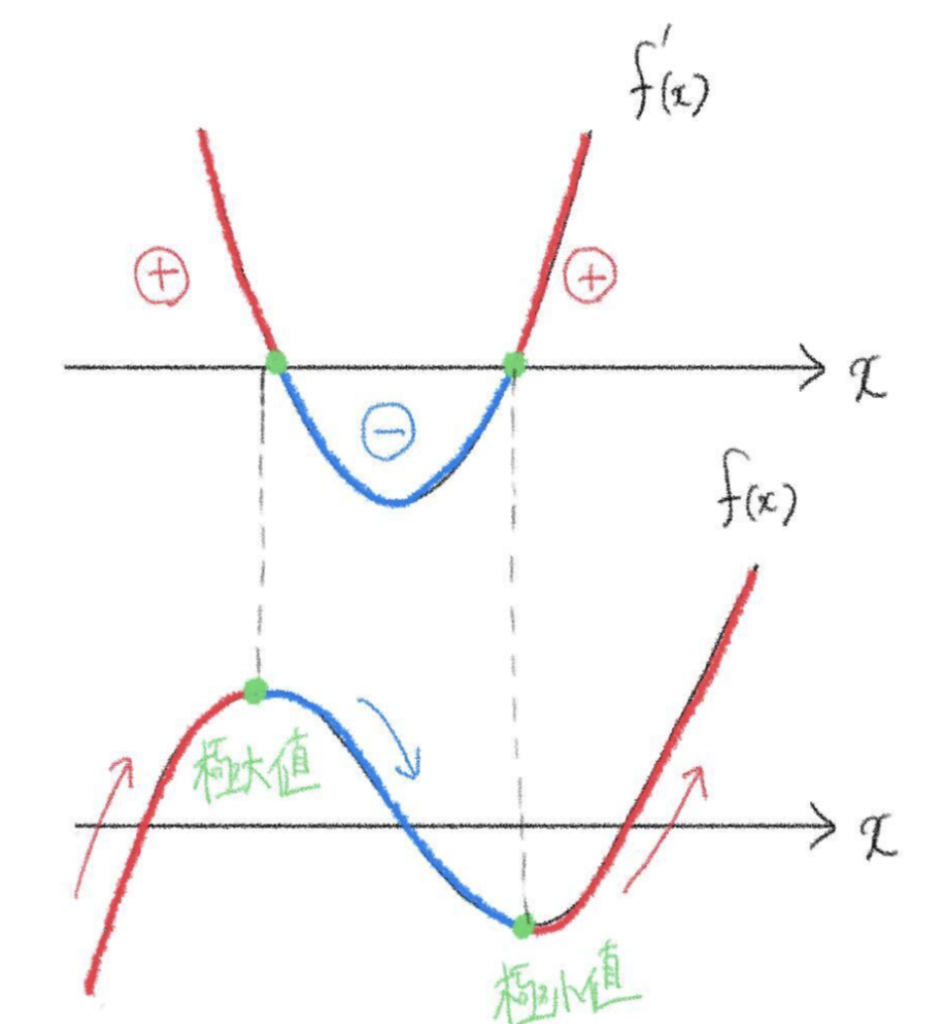
\(x=a\) を境目として \(f'(x)\) が正から負に変われば極大値 \(f(a)\)をとる。
\(x=a\) を境目として \(f'(x)\) が負から正に変われば極小値 \(f(a)\) をとる。
\(f'(x)\) の正負と \(f(x)\) の増減の関係性を掴もう！
関数の極値（問題）
次の関数の極値を求めよ。
(1) \(y=(x^2-3)e^{-x}\)
(2) \(y=|x|\sqrt{x+3}\)
＞＞詳細はこちらから
関数の極値（解説）
(1) \(y=(x^2-3)e^{-x}\)
積の微分
\({f(x)g(x)}’=f'(x)g(x)+f(x)g'(x)\)
\(y’=2xe^{-x}+(x^2-3)(-e^{-x})\)
\(=-(x+1)(x-3)e^{-x}\)
\(y’=0\) とすると、\(x=-1\), \(3\)
増減表は以下のようになる。
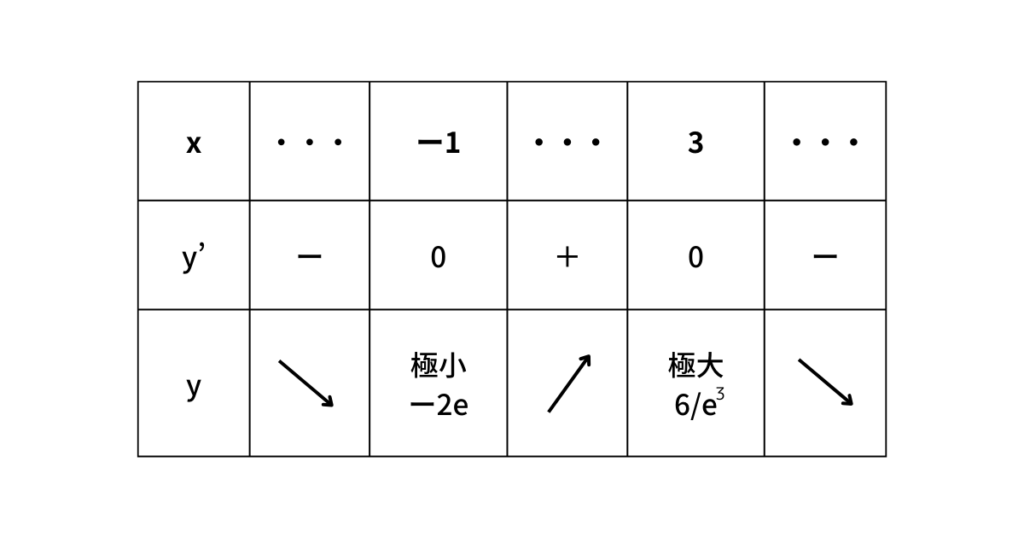
よって、
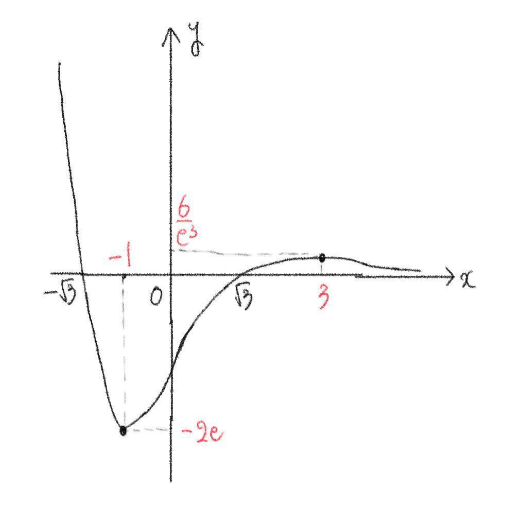
\(x=3\) で極大値 \(\displaystyle\frac{6}{e^3}\)
\(x=-1\) で極小値 \(-2e\)
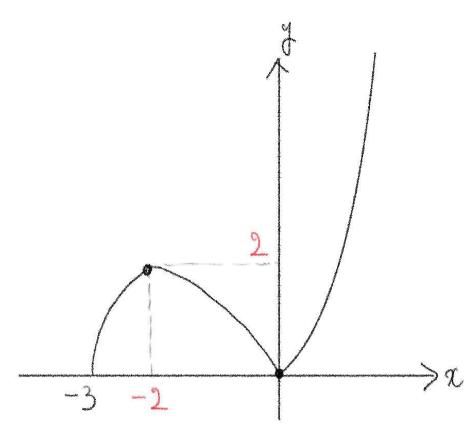
(2) \(y=|x|\sqrt{x+3}\)
定義域は \(x\leq -3\) である。
\(x\leq 0\) のとき、\(y=x\sqrt{x+3}\) であるから、\(x>0\) では
\(y’=\sqrt{x+3}+\displaystyle\frac{x}{2\sqrt{x+3}}\)
\(=\displaystyle\frac{3(x+2)}{2\sqrt{x+3}}\)
ゆえに、\(x>0\) では常に \(y’>0\)
\(-3\leq x<0\) のとき、
\(y=-x\sqrt{x+3}\) であるから、\(-3<x<0\)
では \(y’=-\displaystyle\frac{3(x+2)}{2\sqrt{x+3}}\)
\(y’=0\) とすると \(x=-2\)
増減表は以下のようになる。
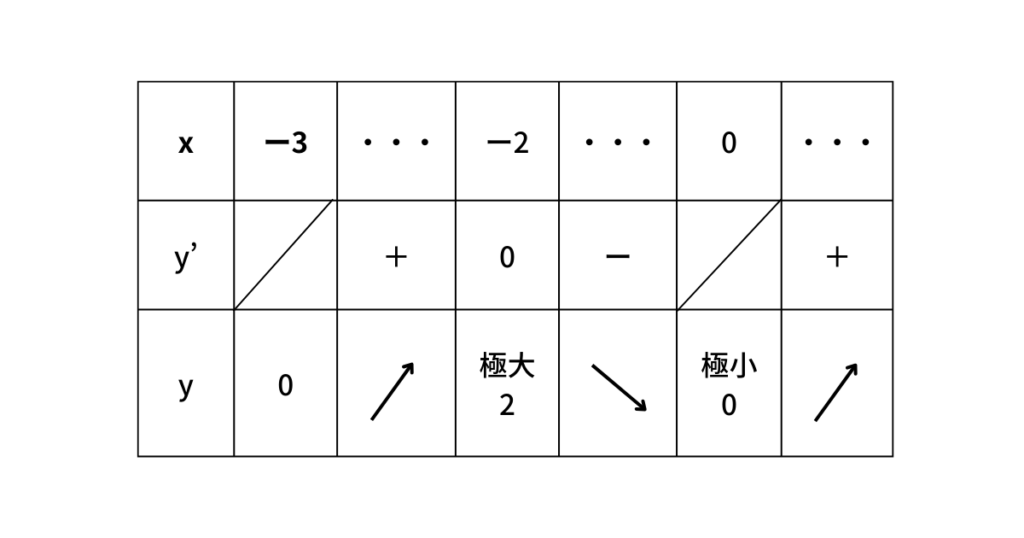
よって
\(x=-2\) で極大値 \(2\)
\(x=0\) で極大値 \(0\)
おわりに
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！