変化率とは？｜平均の変化率と瞬間の変化率

平均変化率とは

「平均の変化率」とは、ある点からある点までの「傾き」のこと。

ある関数 $f(x)$ を考えます。この関数はなんでもOKです。その関数上にある点を $2$ つとります。これを $A(a,f(a))$、$B(b,f(b))$ と書きます。（適当に $2$ 点取っただけです。）

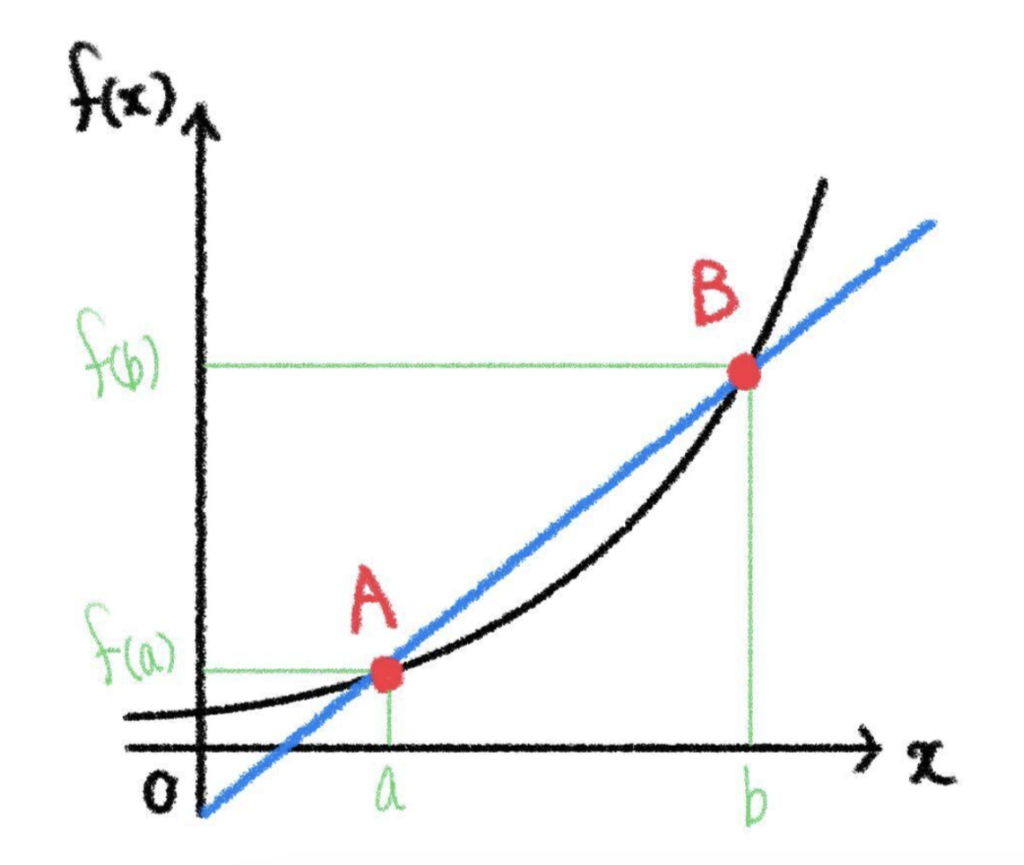
そして、線分 $AB$ を考え、傾きを考えてみます。

${\displaystyle \frac{f(b)-f(a)}{b-a}}$

具体的な問題文に言い換えれば、「地点 $A$ から地点 $B$ までの平均の速度を求めなさい。」などが想定されます。

中学の範囲では、これを直線の傾きと呼んでいましたが、微分という単元の範囲の中では。$x$ が $a$ から $b$ まで変化するときの平均変化率と呼びます。

ここまではあくまでも $2$ 点間の変化率を求めました。次は、ある $1$ つの点に着目したときの変化具合（変化率）を考えます。その際に使う考え方が瞬間の変化率。言い換えると微分です。

瞬間変化率とは

「瞬間の変化率」とは、その名の通り”瞬間”の変化具合のことです。

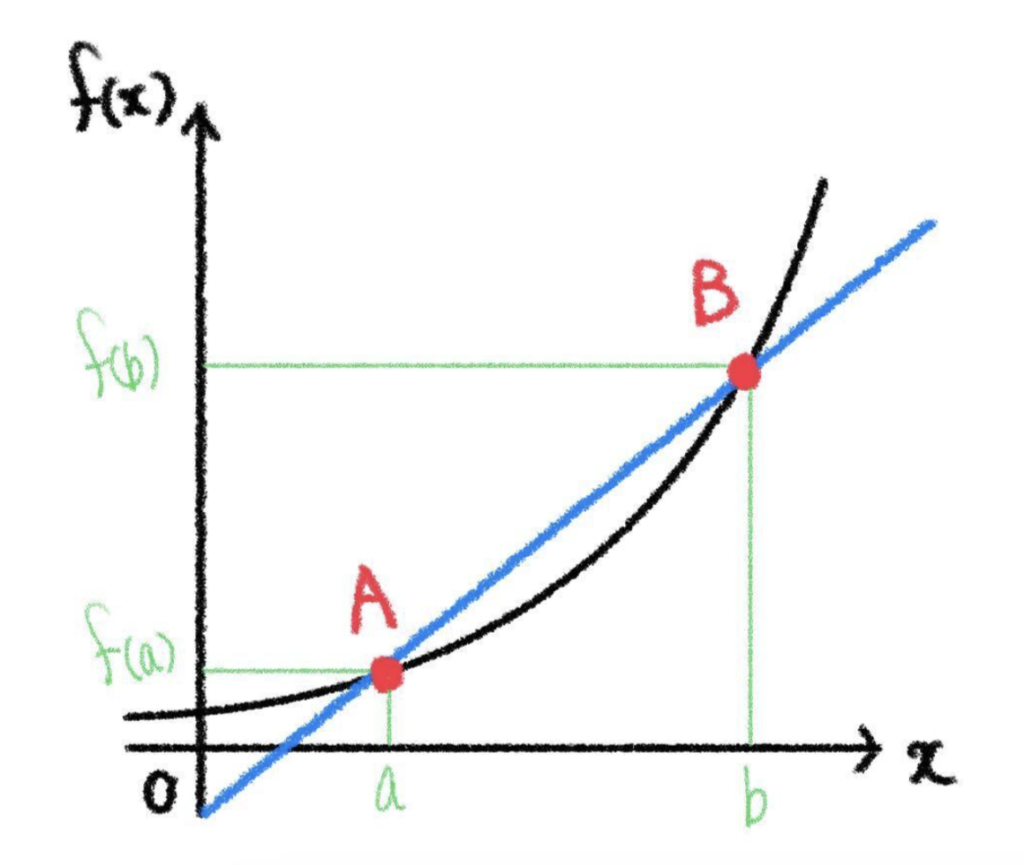
図の直線の傾き

${\displaystyle \frac{f(b)-f(a)}{b-a}}$

の $a$ と $b$ の差をどんどん縮めていきます。そして限りなく $b$ が $a$ に近づいたとします。それを、

${\displaystyle \underset{b\to a}{lim}\frac{f(b)-f(a)}{b-a}}$

と書きます。ここの時点でよくわからないよ〜って人は以下の記事を見てみてください。

そして、この $b$ と $a$ の差、すなわち $b-a$ を $h$ と置くと、

${\displaystyle \underset{h\to 0}{lim}\frac{f(a+h)-f(a)}{h}}$

と書けます。ここで具体的な例を示してみます。

---

新幹線のある時刻における瞬間の速度を求めたい場合、式は以下のようになります。

速度 ($v$)$=$ 位置の変化 ($x$) ／ 時刻の変化 $(t$)

小学校で習った「みはじ（きはじ）」を思い出せば良いですね。

しかし、このままでは平均の速度になってしまいます。つまり、ある場所からある場所まで移動した時の速度になります。そこで、瞬間の速度を求められるように式を変形します。

例えば、位置を $y$、時刻を $x$ として、$y=x^2$ で表されるとします。
時刻 $x$ が $a$ から $a+h$ まで変化すると、速度 $v$ は次の式で求められます。

$v={\displaystyle \frac{(a+h{)}^2-a^2}{(a+h)-a}}$
　$={\displaystyle \frac{a^2+2ah+h^2-a^2}{a+h-a}}$
　$={\displaystyle \frac{2ah+h^2}{h}}$
　$=2a+h$

ここで、「瞬間の変化率」というのは、「時刻の変化量 $h$ を極力 $0$ に近づけたい」ということです。

それを、極限の記号を用いて、

${\displaystyle \underset{h\to 0}{lim}(2a+h)}$

と書いたりします。今回はシンプルに $h$ に $0$ を代入します。そうすると、「$2t$」が得られます。

これが瞬間の変化率であり、微分した値になります。これを、$y^{\prime }=2t$ と表したりします。

微分の定義を詳しく説明した記事もあるのであわせてご覧ください。

おわりに