このページでは、指数関数のグラフの描き方を詳しく解説していきます！
・\(y=2^x\)
・\(y=\big(\displaystyle\frac{1}{3}\big)^x\)
・\(y=1+2\cdot 3^{x-1}\)
などのグラフを素早く描けるようにしましょう！
指数関数 \(y=2^x\) のグラフ
まずは、 \(x\) に順番に値を代入してみる。
\(x=-4\) のとき、\(y=\frac{1}{16}\)
\(x=-3\) のとき、\(y=\frac{1}{8}\)
\(x=-2\) のとき、\(y=\frac{1}{4}\)
\(x=-1\) のとき、\(y=\frac{1}{2}\)
\(x=0\) のとき、\(y=1\)
\(x=1\) のとき、\(y=2\)
\(x=2\) のとき、\(y=4\)
\(x=3\) のとき、\(y=8\)
\(x=4\) のとき、\(y=16\)
\(x\) の値を大きくしていくと、\(y\) の値は加速度を増して大きくなる様子がわかります
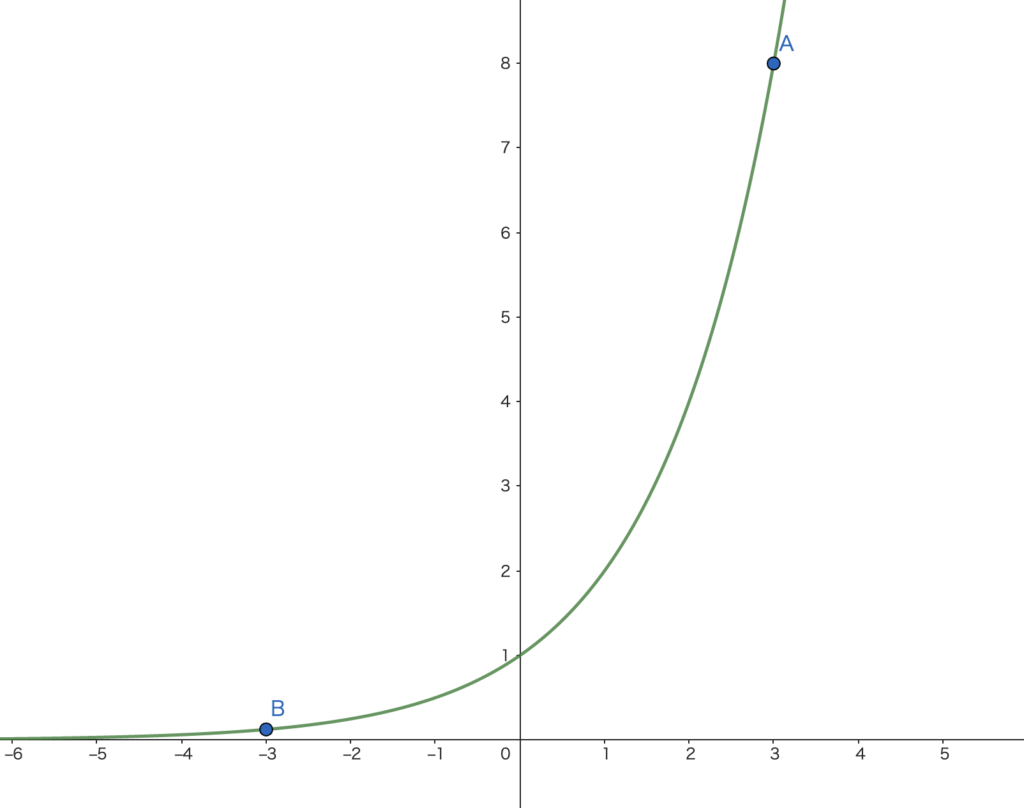
指数関数 \(y=a^x\) のグラフ
\(a>1\) のとき
・\(x\) が十分小さいとき（点 \(B\)）、\(y\) は限りなく \(0\) に近い。
※ \(0\) に交わることはない。
・\(x=0\) のとき \(y=1\)
・\(x\) が十分大きいとき（点 \(A\)）、\(y\) は非常に大きくなる。
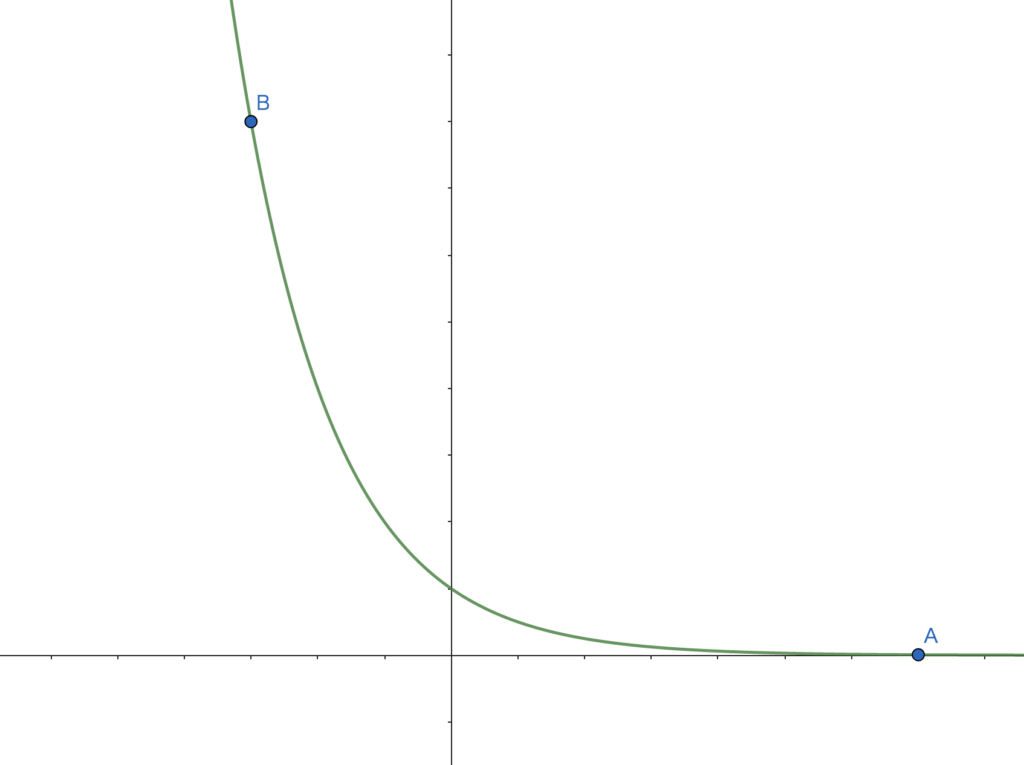
\(0<a<1\) のとき
・\(x\) が十分小さいとき（点 \(B\)）、\(y\) は爆発的に大きい
・\(x=0\) のとき、\(y=1\)
・\(x\) が十分大きいとき（点 \(A\)）、\(y\) は \(0\) に近い
＞＞詳細はこちらから
指数関数のグラフ（発展）
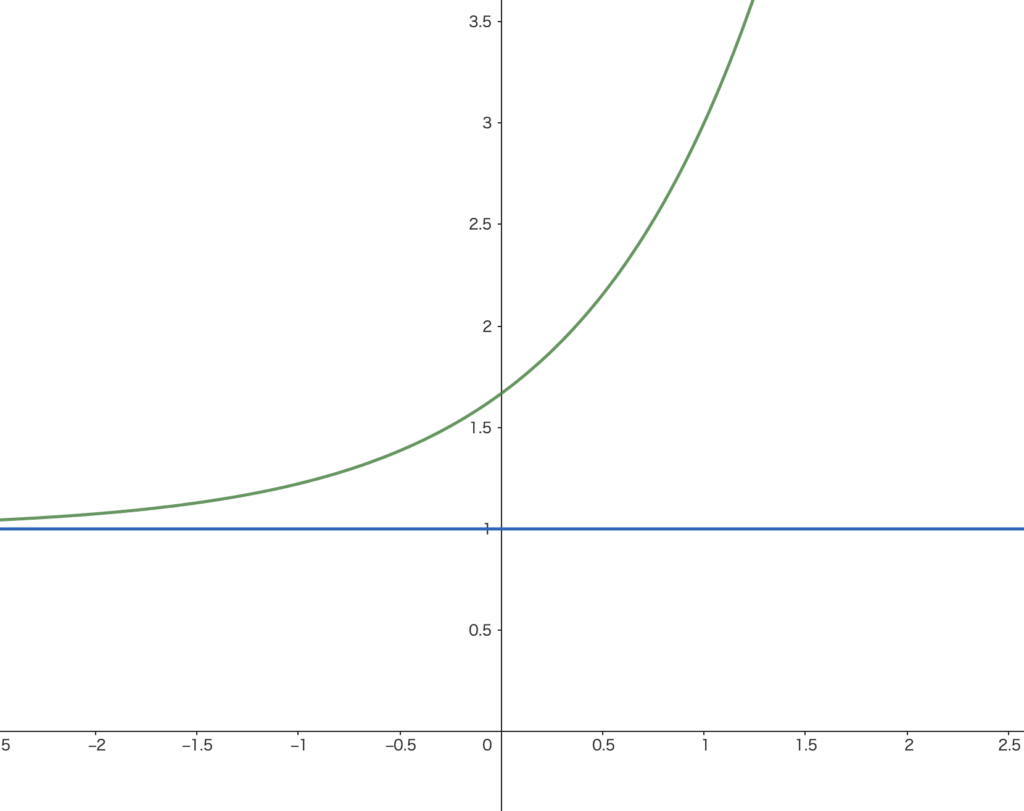
\(y=1+2\cdot 3^{x-1}\) のグラフ
・\(y\) 軸方向に \(+1\)
→\(y=1\) が漸近線（青線）
・\(x\) の値が十分に小さいとき、\(y\) は \(1\) に近い
・\(2\cdot 3^{x-1}\) について、\(3^{x-1}\) を \(2\) 倍している。しかし、グラフを描く際はそこまで気にする必要はない。
おわりに
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！