位置ベクトル
今回は位置ベクトルについての問題を扱っていきます。
ポイントは２点！
① 位置ベクトルとは？を理解する！
② 式を図に落とし込む！
位置ベクトルの概念をしっかりと理解し、式を図に落とし込むことが重要です！
位置ベクトルとは？
簡単に言えば、位置ベクトルとは「始点と終点が設定されたベクトル」と思っておけばOKです！
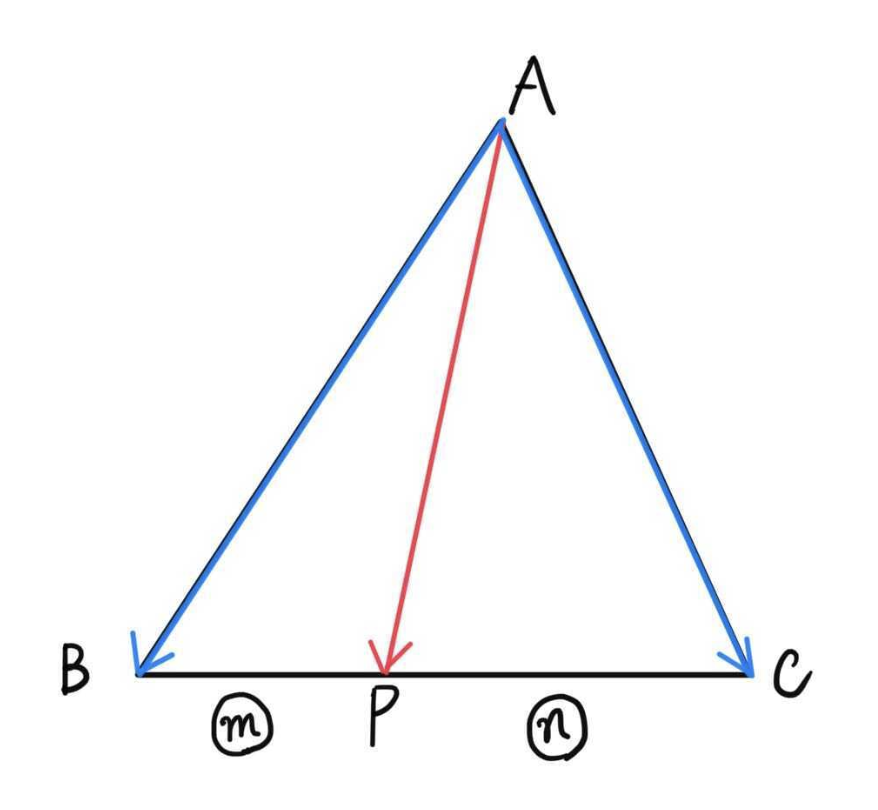
\(\triangle{ABC}\) において、線分 \(BC\) を \(m:n\) に内分する点を \(P\) とするとき、
\(\overrightarrow{AP}=\displaystyle\frac{n}{m+n}\overrightarrow{AB}+\frac{m}{m+n}\overrightarrow{AC}\)
式を図に落とし込むポイント
式を図に落とし込むために、始点を変更しなければいけない場合があります。
始点の変更についてはこちらをチェック
位置ベクトル（問題）
\(\triangle{ABC}\) の内部に点 \(P\) があり、
\(6\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}\)
を満たすとき、点 \(P\) はどのような位置にあるか。
＞＞詳細はこちらから
答案の例
\(-6\overrightarrow{AP}+3\overrightarrow{AB}-3\overrightarrow{AP}+2\overrightarrow{AC}-2\overrightarrow{AP}=\overrightarrow{0}\)
\(-11\overrightarrow{AP}+3\overrightarrow{AB}+2\overrightarrow{AC}=\overrightarrow{0}\)
\(-11\overrightarrow{AP}=-3\overrightarrow{AB}-2\overrightarrow{AC}\)
\(\overrightarrow{AP}=\displaystyle\frac{3}{11}\overrightarrow{AB}+\frac{2}{11}\overrightarrow{AC}\)
\(\overrightarrow{AP}=\displaystyle\frac{5}{11}\left(\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\right)\)
\(\overrightarrow{AD}=\displaystyle\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\)
とおくと、点 \(D\) は、\(\triangle{ABC}\) において線分 \(BC\) を \(2:3\) に内分する点とわかる。\(\cdots\) ①
① より
また、\(\overrightarrow{AP}=\displaystyle\frac{5}{11}\overrightarrow{AD}\)
と表されるので、点 \(P\) は、\(\triangle{ABC}\) において線分 \(AD\) を \(5:6\) に内分する点とわかる。 \(\cdots\) ②
② より
以上、①と②を整理して書くと、線分 \(BC\) を \(2:3\) に内分する点を \(D\) とすると、点 \(P\) は線分 \(AD\) を \(5:6\) に内分する点である。
解説
今回の問題では、
式：\(6\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}\)
図：\(\triangle{ABC}\)
上記の式を図に落とし込む必要があります。
そのためにまずは始点を変更してみましょう。今回の問題の式を見てみると、始点が \(P\) になっていますね。このままだと点 \(P\) の位置がよくわかりません。
点 \(P\) の位置をわかりやすくするためには、三角形の頂点（点\(A\)）を始点にしましょう。
\(-6\overrightarrow{AP}+3\overrightarrow{AB}-3\overrightarrow{AP}+2\overrightarrow{AC}-2\overrightarrow{AP}=\overrightarrow{0}\)
\(-11\overrightarrow{AP}+3\overrightarrow{AB}+2\overrightarrow{AC}=\overrightarrow{0}\)
\(-11\overrightarrow{AP}=-3\overrightarrow{AB}-2\overrightarrow{AC}\)
\(\overrightarrow{AP}=\displaystyle\frac{3}{11}\overrightarrow{AB}+\frac{2}{11}\overrightarrow{AC}\)
\(\overrightarrow{AP}=\displaystyle\frac{5}{11}\left(\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\right)\)
ここまで整理できたら、図に落とし込みましょう。
\(\overrightarrow{AD}=\displaystyle\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\)
とおくと、点 \(D\) は、\(\triangle{ABC}\) において線分 \(BC\) を \(2:3\) に内分する点とわかる。\(\cdots\) ①
① より
また、\(\overrightarrow{AP}=\displaystyle\frac{5}{11}\) \(\left(\displaystyle\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\right)\)
に \(\overrightarrow{AD}=\) \(\displaystyle\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\) を代入すると、
\(\overrightarrow{AP}=\displaystyle\frac{5}{11}\overrightarrow{AD}\)
と表されるので、ここまで整理できたら、図に落とし込みましょう。
② より
①：点 \(D\) は、\(\triangle{ABC}\) において線分 \(BC\) を \(2:3\) に内分する点とわかる。
②：点 \(P\) は、\(\triangle{ABC}\) において線分 \(AD\) を \(5:6\) に内分する点とわかる。
以上、①と②を整理して書くと、
線分 \(BC\) を \(2:3\) に内分する点を \(D\) とすると、点 \(P\) は線分 \(AD\) を \(5:6\) に内分する点である。
おわりに
今回は、位置ベクトルについての問題でした。
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！