連立不等式
今回は連立不等式について解説していきます！
まずは、不等式が表してることを確認していきましょう。
不等式 \(2x-3<3\)
これが表してるのは、「\(2x-3<3\) を満たす \(x\) の範囲」となります。
連立不等式
$$\begin{cases}2x-3<3\\x>6\end{cases}$$
このように、複数の不等式が連なってる場合は、各不等式が表す範囲の共通部分を答える必要があります。
今回の問題を通して、解けるだけでなく連立不等式の意味をしっかりと理解しましょう。
連立不等式を日本語に言い換えてみる
式の意味を日本語で示すことができればやるべきことが一気に見えてきます。
連立不等式
$$\begin{cases}5x+1\leq 8(x+2)\\2x-3<1-(x-5)\end{cases}$$
を解け。
これを言い換えると、
と言い換えることができます。
解法の手順
連立不等式の解法の手順
\(\begin{cases}5x+1\leq 8(x+2)\\2x-3<1-(x-5)\end{cases}\)
STEP１ それぞれの不等式の解を求めます。
STEP２ それぞれの不等式の解を図にします。
STEP３ 図を見て、それぞれの不等式の解の共通部分を求めます。
連立不等式（問題）
連立不等式
$$\begin{cases}5x+1\leq 8(x+2)\\2x-3<1-(x-5)\end{cases}$$
を解け。
＞＞詳細はこちらから
答案の例
\(5x+1\leq 8(x+2)\)
\(5x+1\leq 8x+16\)
\(5x-8x\leq 16-1\)
\(-3x\leq 15\)
\(x\geq -5\) \(\cdots\) ①
\(2x-3<1-(x-5)\)
\(2x-3<1-x+5\)
\(2x-3<-x+6\)
\(2x+x<6+3\)
\(3x<9\)
\(x<3\) \(\cdots\) ②
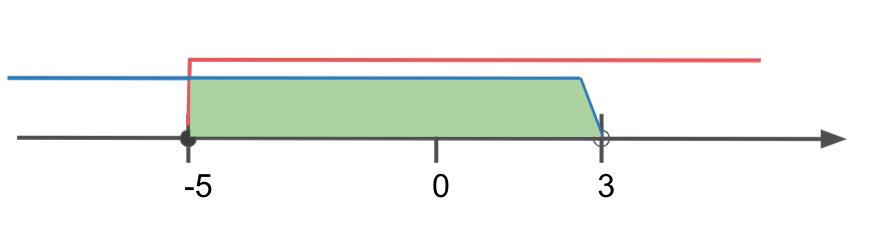
よって、① と ② 両方を満たす \(x\) の範囲は、
\(-5\leq x <3\)
解説
連立不等式
\(\begin{cases}5x+1\leq 8(x+2)\\2x-3<1-(x-5)\end{cases}\)
を解くとは、
「\(5x+1\leq 8(x+2)\) と \(2x-3<1-(x-5)\) それぞれの不等式の解の共通部分を求める」ということです。
\(5x+1\leq 8(x+2)\) と \(2x-3<1-(x-5)\) それぞれの不等式の解を求める。
\(5x+1\leq 8(x+2)\)
\(5x+1\leq 8x+16\)
\(5x-8x\leq 16-1\)
\(-3x\leq 15\)
\(x\geq -5\) \(\cdots\) ①
\(2x-3<1-(x-5)\)
\(2x-3<1-x+5\)
\(2x-3<-x+6\)
\(2x+x<6+3\)
\(3x<9\)
\(x<3\) \(\cdots\) ②
数直線により共通部分を求める
①, ② それぞれを数直線上に表す。
図
よって、① と ② 両方を満たす \(x\) の範囲は、
\(-5\leq x <3\)
おわりに
今回は、連立不等式でした。
連立不等式の意味は理解できましたか？これまで連立不等式を解く問題を機械的に計算するだけになっていた人は、連立不等式の意味をしっかりと理解した上で解けるようになりましょう。そうすると、応用問題にも太刀打ちできるようになります。
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！