等式を満たす点の位置
今回は空間ベクトルの問題です！
空間図形になると難しく感じるかもしれませんが、考え方は平面と同様ですし、適宜空間図形を切り取れば平面図形として見ることができます。例題と解説を用意してるので解いてみてください。
等式を満たす点の位置（問題）
四面体 \(ABCD\) に関し、次の等式を満たす点 \(P\) はどのような位置にある点か。
\(\overrightarrow{AP}+3\overrightarrow{BP}+2\overrightarrow{CP}+6\overrightarrow{DP}=\overrightarrow{0}\)
＞＞詳細はこちらから
解説
\(\overrightarrow{AP}+3\overrightarrow{BP}+2\overrightarrow{CP}+6\overrightarrow{DP}=\overrightarrow{0}\)
\(\overrightarrow{AP}+3(\overrightarrow{AP}-\overrightarrow{AB})+2(\overrightarrow{AP}-\overrightarrow{AC})\)
\(+6(\overrightarrow{AP}-\overrightarrow{AD})=\overrightarrow{0}\)
\(\overrightarrow{AP}+3\overrightarrow{AP}-3\overrightarrow{AB}+2\overrightarrow{AP}-2\overrightarrow{AC}\)
\(+6\overrightarrow{AP}-6\overrightarrow{AD}=\overrightarrow{0}\)
\(12\overrightarrow{AP}-3\overrightarrow{AB}-2\overrightarrow{AC}-6\overrightarrow{AD}=\overrightarrow{0}\)
\(12\overrightarrow{AP}=3\overrightarrow{AB}+2\overrightarrow{AC}+6\overrightarrow{AD}\)
\(\overrightarrow{AP}=\displaystyle\frac{1}{12}(3\overrightarrow{AB}+2\overrightarrow{AC}+6\overrightarrow{AD})\)
この形を目指す
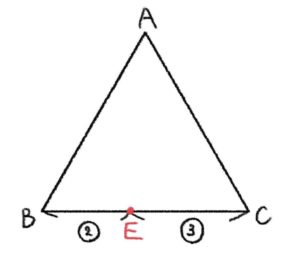
\(\triangle{ABC}\) において、線分 \(BC\) を \(m:n\) に内分する点を \(P\) とするとき、
\(\overrightarrow{AP}=\displaystyle\frac{n}{m+n}\overrightarrow{AB}+\frac{m}{m+n}\overrightarrow{AC}\)
\(\overrightarrow{AP}=\displaystyle\frac{1}{12}\left\{5\cdot \left(\frac{3\overrightarrow{AB}+2\overrightarrow{AC}}{5}\right)+6\overrightarrow{AD}\right\}\)
\(\overrightarrow{AE}=\displaystyle\frac{3\overrightarrow{AB}+2\overrightarrow{AC}}{5}\) とおくと、
\(\overrightarrow{AP}=\displaystyle\frac{1}{12}\left\{5\overrightarrow{AE}+6\overrightarrow{AD}\right\}\)
\(\overrightarrow{AP}=\displaystyle\frac{1}{12}\left\{11\cdot \left(\frac{5\overrightarrow{AE}+6\overrightarrow{AD}}{11}\right)\right\}\)
\(\overrightarrow{AF}=\displaystyle\frac{5\overrightarrow{AE}+6\overrightarrow{AD}}{11}\) とおくと、
\(\overrightarrow{AP}=\displaystyle\frac{11}{12}\overrightarrow{AF}\)
図を描く手順
手順①
\(\overrightarrow{AE}=\displaystyle\frac{3\overrightarrow{AB}+2\overrightarrow{AC}}{5}\)
三角形 \(ABC\) に着目して平面図形として見る。
手順②
\(\overrightarrow{AF}=\displaystyle\frac{5\overrightarrow{AE}+6\overrightarrow{AD}}{11}\)
次に三角形 \(AED\) に着目する。
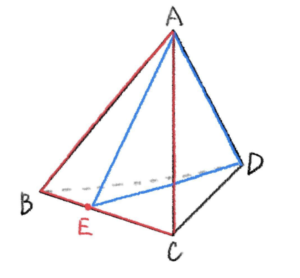
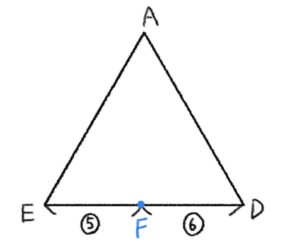
手順③
\(\overrightarrow{AP}=\displaystyle\frac{11}{12}\overrightarrow{AF}\)
手順①, ② より導いた点 \(F\)より、以下のように描かれる。
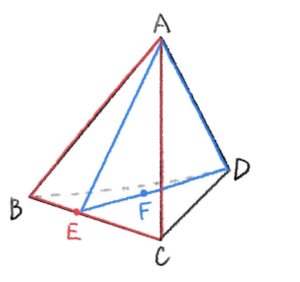
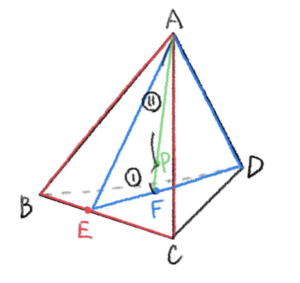
以上より、点 \(P\) は線分 \(BC\) を \(2:3\) に内分する点を点 \(E\) とし、線分 \(ED\) を \(5:6\) に内分する点を点 \(F\) とするとき、線分 \(AF\) を \(11:1\) に内分する点である。
おわりに
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！