集合の意味
集合
→属していることがはっきりしているものの集まり。\(A\), \(B\) などの大文字で表す。
要素
→集合に属する \(1\) つ \(1\) つのもの。
\(a \in A\) \(\Longleftrightarrow\) \(a\) は集合 \(A\) の要素である
\(b \notin A\) \(\Longleftrightarrow\) \(b\) は集合 \(A\) の要素でない
集合の表し方
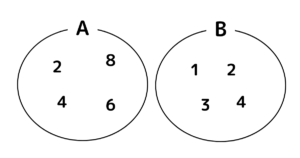
(1) 要素を書き並べて表す。
(2) 要素の満たす条件を述べて表す。
例えば、\(1\) 桁の正の偶数の集合 \(A\) は、
(1) では、
\(A=\{2\), \(4\), \(6\), \(8\}\)
(2) では、
\(A=\{x\) | \(n\) は整数, \(1\leq n\leq 4\}\) など
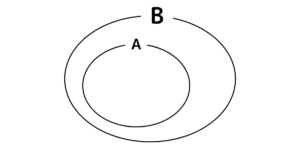
部分集合
\(A\) は \(B\) の部分集合である
\(\Longleftrightarrow\) \(A \subset B\)
\(\Longleftrightarrow\) \(x\in A\) ならば \(x\in B\)
\(A\) と \(B\) は等しい
\(\Longleftrightarrow\) \(A=B\)
\(\Longleftrightarrow\) \(A\subset B\) かつ \(B\subset A\)
※全く同じ集合ということ
共通部分と和集合
＞＞詳細はこちらから
共通部分（交わり）
→ \(A\cap B=\{x\) | \(x\in A\) かつ \(x\in B\}\)
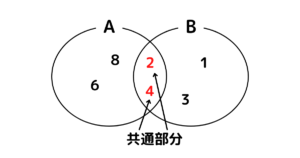
和集合（結び）
→ \(A\cup B=\{x\) | \(x\in A\) または \(x\in B\}\)
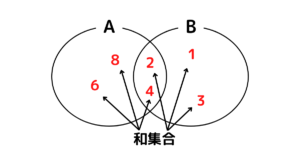
全体集合
→ あらかじめ考えているものの全体の集合
空集合
→ 要素を \(1\) つももたない集合。\(\emptyset\) で表す。空集合は、すべての集合の部分集合である。
補集合
補集合
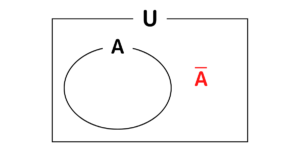
→ 全体集合 \(U\) に属し、\(U\) の部分集合 \(A\) に属さない要素全体の集合。\(\bar{A}\) で表す。
\(\bar{A}=\{x\) | \(x\in U\) かつ \(x\notin A\}\)
とくに、\(A\cap \bar{A}=\emptyset\), \(A\cap \bar{A}=U\)
ド・モルガンの法則
\(\overline{A\cap B}=\bar{A}\cup \bar{B}\)
図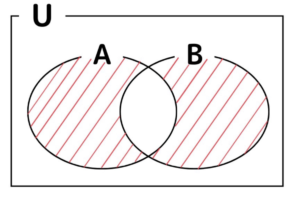
\(\overline{A\cup B}=\bar{A}\cap \bar{B}\)
図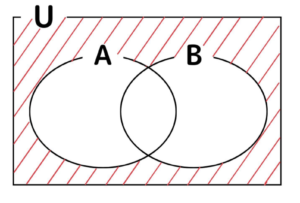
集合の要素の個数
集合 \(A\) の要素の個数を \(n(A)\) で表す。
(1) \(n(A\cup B)=n(A)+n(B)-n(A\cap B)\)
(2) \(A\cap B=\emptyset\) のとき、\(n(A\cup B)=n(A)+n(B)\)
(3) \(n(\bar{A})=n(U)-n(A)\)
おわりに
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！