複素数とは、\(a+bi\) (\(a\), \(b\) は実数)で表されます。
これまで扱ってきた実数に虚数が追加された数字のことを言います。
複素数範囲に拡張された因数分解
虚数とは
虚数とは英語で imaginary number といい、2乗したときに0未満の実数になる数を指します。
代表的なのが虚数単位「\(i\)」で
となります。英語を直訳すると「想像上の数」 であることからも分かる通り、このような数は現実には存在しません。
複素数とは
複素数とは、実数と虚数を合わせたものです。
\(1+3i\) や \(-2+5i\) など \(\spadesuit+\clubsuit i\) のような形で表します。
これまでは、実数範囲でしか数を扱ってきませんでした、複素数範囲になって数が拡張されたイメージを持ちましょう。図にするとこんな感じです。
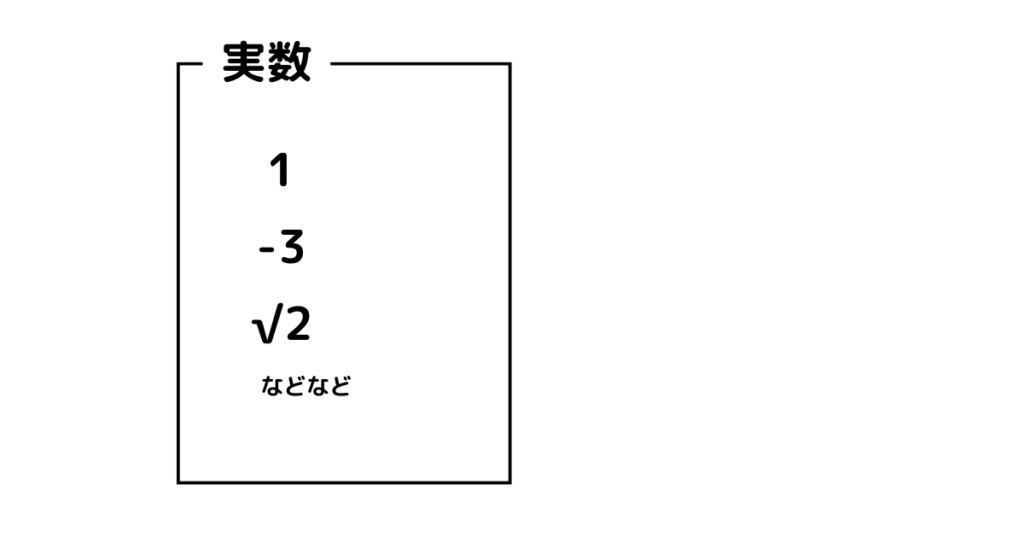
これまでの実数範囲はこんな感じです。これが知ってる数字の全てだったと思います。
複素数を学ぶことで赤い部分が追加されました。問題などで扱う数字が増えるというイメージです。
複素数範囲に拡張された因数分解（例題）
次の式を、複素数の範囲で因数分解せよ。
(1) \(2x^2-3x+4\)
(2) \(x^4-64\)
(3) \(x^4+4x^2+36\)
＞＞詳細はこちらから
解説
(1)
実数範囲だと因数分解不可
\(2x^2-3x+4=0\) とおくと
\(x=\displaystyle\frac{3\pm\sqrt{-23}}{4}\)
\(=\displaystyle\frac{3\pm\sqrt{23}i}{4}\)
よって、
\(=\left(x-\displaystyle\frac{3-\sqrt{23}i}{4}\right)\left(x-\displaystyle\frac{3+\sqrt{23}i}{4}\right)\)
(2)
\(x^4-64\)
\(=(x^2+8)(x^2-8)\)
\(=(x^2+8)(x+2\sqrt{2})(x-2\sqrt{2})\)
実数範囲だとここで因数分解終了
\(x^2+8=0\) とおくと、
\(x^2=-8\)
\(x=\pm 2\sqrt{2}i\) より
\(=(x+2\sqrt{2}i)(x-2\sqrt{2}i)(x+2\sqrt{2})(x-2\sqrt{2})\)
(3)
\(x^4+4x^2+36\)
\(=x^4+12x^2-8x^2+36\)
\(=x^4+12x^2+36-8x^2\)
\(=(x^2+6)^2-8x^2\)
\(=(x^2+6-2\sqrt{2}x)(x^2+6+2\sqrt{2}x)\)
\(=(x^2-2\sqrt{2}x+6)(x^2+2\sqrt{2}x+6)\)
実数範囲だとここで因数分解終了
\(\cdot\) \(x^2-2\sqrt{2}x+6=0\) について
\(x=\displaystyle\frac{2\sqrt{2}\pm\sqrt{8-24}}{2}\)
\(x=\displaystyle\frac{2\sqrt{2}\pm\sqrt{-16}}{2}\)
\(x=\displaystyle\frac{2\sqrt{2}\pm 4i}{2}\)
\(x=\sqrt{2}\pm 2i\)
\(\cdot\) \(x^2+2\sqrt{2}x+6=0\) について
\(x=\displaystyle\frac{-2\sqrt{2}\pm\sqrt{8-24}}{2}\)
\(x=\displaystyle\frac{-2\sqrt{2}\pm\sqrt{-16}}{2}\)
\(x=\displaystyle\frac{-2\sqrt{2}\pm 4i}{2}\)
\(x=-\sqrt{2}\pm 2i\)
\(=(x-\sqrt{2}-2i)(x-\sqrt{2}+2i)(x+\sqrt{2}-2i)(x+\sqrt{2}+2i)\)
おわりに
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！