任意の直線 \(\ell\) と三角形 \(ABC\) において、直線 \(\ell\) と \(BC\)、\(CA\)、\(AB\) の交点をそれぞれ \(D\)、\(E\)、\(F\) とする。この時、次の等式が成立する。
\(\displaystyle\frac{AF}{FB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}=1\)
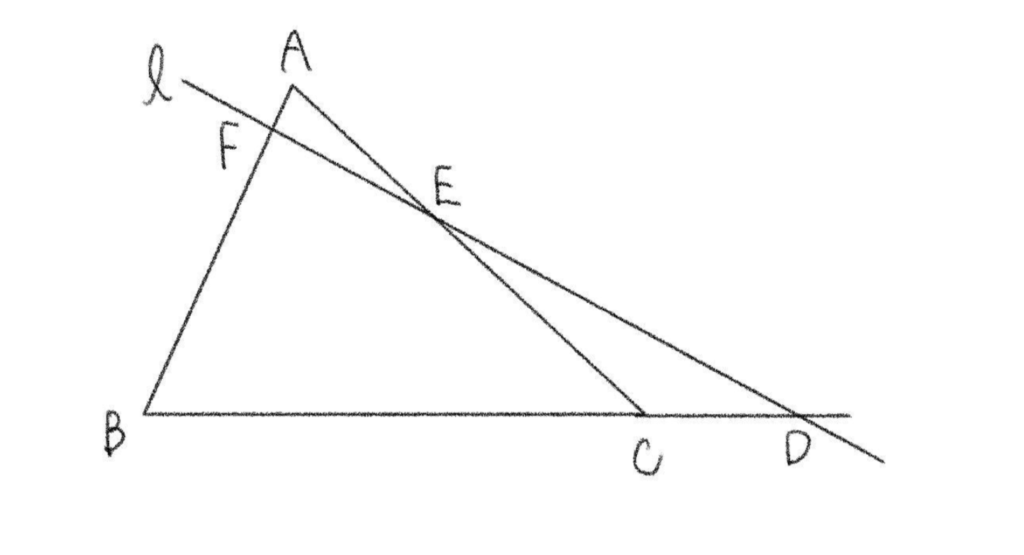
メネラウスの定理の覚え方
覚え方 ① 図の頂点の流れで覚える。
覚え方 ② 定理の日本語をセットで覚える
※片方だけでなく両方を意識して覚えると良いです。①だけ覚えてる方が多いですが、それだけだと形が少し変わっただけで対応できなくなるので両方覚えておくのがおすすめです。
覚え方 ① 図の頂点の流れで覚える
下の図のように、点 \(A\) をスタート地点とし、そこから分数の分子 → 分母の順番で繋がっていくように定理を作っていきます。
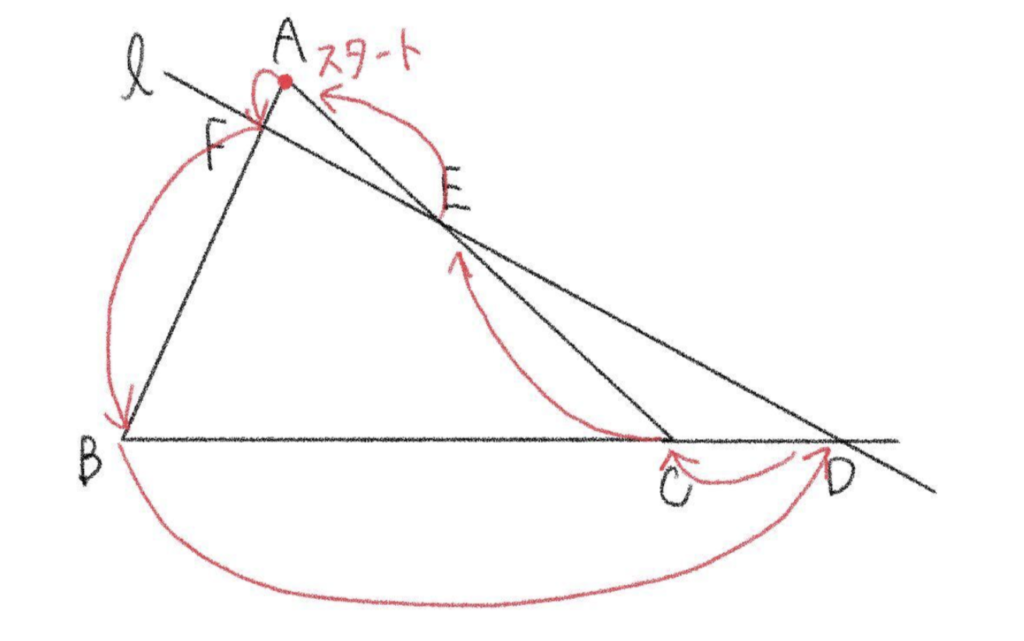
\(\displaystyle\frac{AF}{FB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}=1\)
覚え方 ② 定理の日本語をセットで覚える
任意の直線 \(\ell\) と三角形 \(ABC\) において、直線 \(\ell\) と \(BC\)、\(CA\)、\(AB\) の交点をそれぞれ \(D\)、\(E\)、\(F\) とする。この時、次の等式が成立する。
「任意の直線 \(\ell\) と三角形 \(ABC\)において」を簡単な言葉で言い換えると、「なんでもいいので真っ直ぐな線 \(\ell\) と三角形 \(ABC\) を用意する」となります。
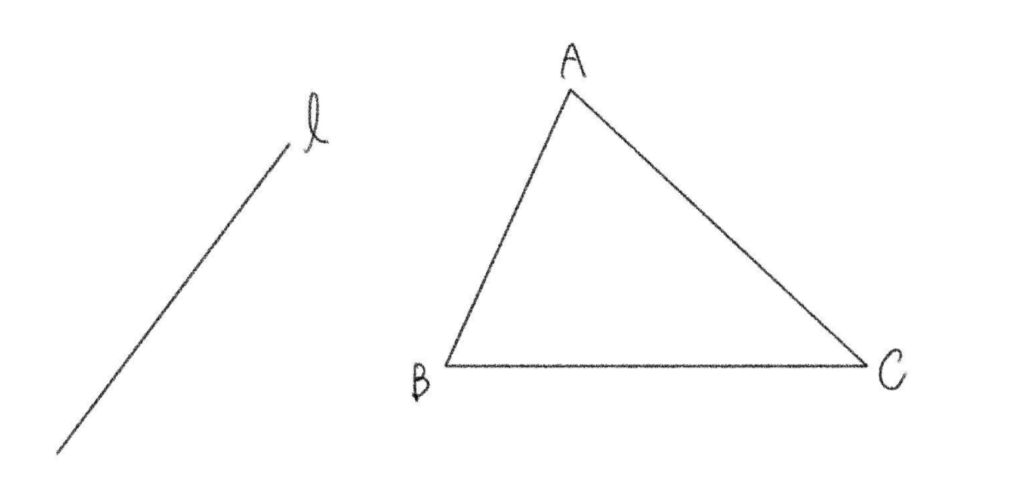
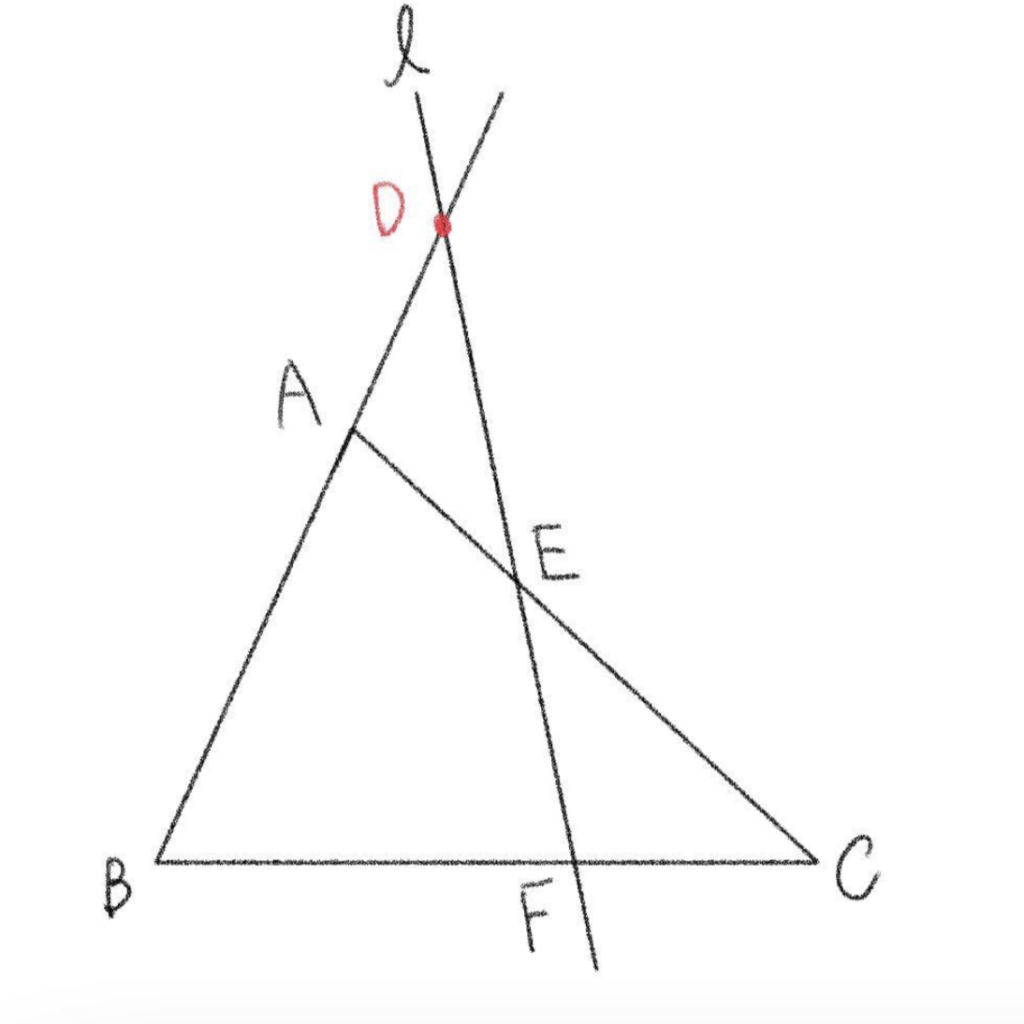
「直線 \(\ell\) と\(BC\)、\(CA\)、\(AB\) の交点をそれぞれ \(D\)、\(E\)、\(F\) とする。」このとき、\(BC\)、\(CA\)、\(AB\) は線分ではなく直線であることに注意しましょう。つまり、下の図のように 直線 \(\ell\) は \(BC\) を横に伸ばした部分と交わっていればいいということです。
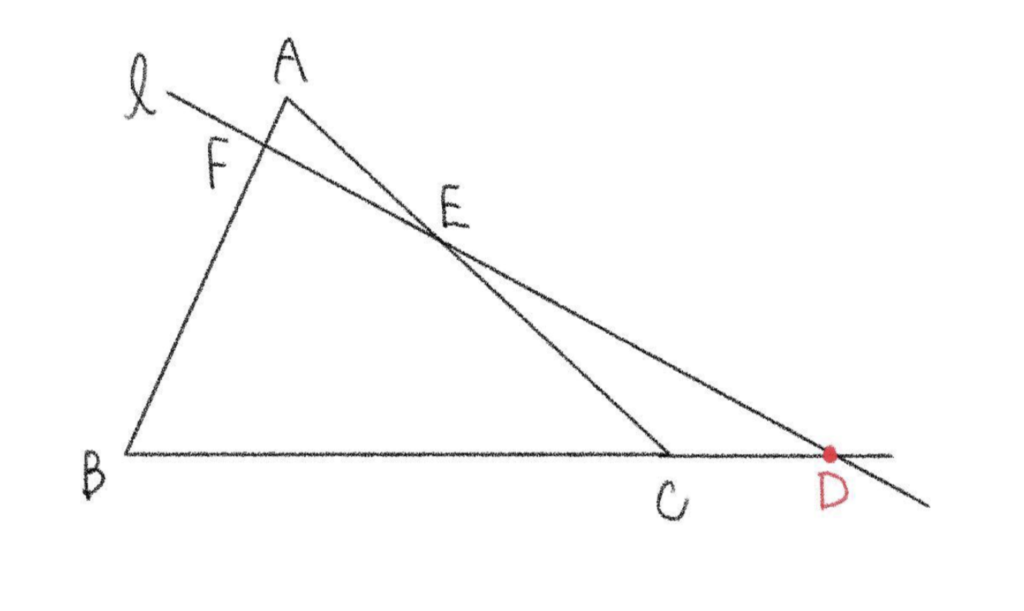
交わる部分は、他の辺を伸ばした部分でもいいわけですので、以下のように直線 \(AB\) 上と交わるような形であってもメネラウスの定理は適用されます。
メネラウスの定理の証明
下の図のように、直線 \(ell\) が \(triangle{ABC}\) の辺 \(BC\), \(CA\), \(AB\) またはその延長と点 \(D\), \(E\), \(F\) で交わるとする。
頂点 \(A\), \(B\), \(C\) から直線 \(\ell\) に垂線 \(AL\), \(BM\), \(CN\) を引く。
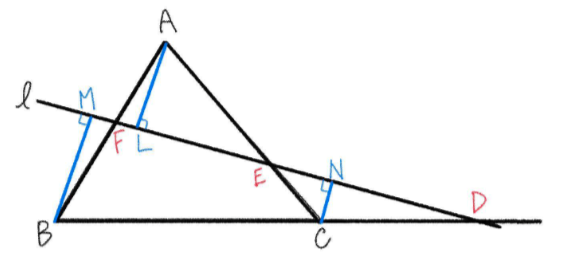
線分 \(BM\), \(AL\), \(CN\) は平行より
\(\triangle{AFL}\sim\triangle{BFM}\)\(\cdots\) ①
\(\triangle{MBD}\sim\triangle{NCD}\)\(\cdots\) ②
\(\triangle{ALE}\sim\triangle{CNE}\)\(\cdots\) ③
※ 「\(\sim\)」は相似記号
①より \(AF:BF==AL:BM\)
\(AF\cdot BM=BF\cdot AL\)
$$\displaystyle\frac{AF}{BF}=\frac{AL}{BM}\cdots ④$$
②より \(BD:CD=BM:CN\)
\(CD\cdot BM=BD\cdot CN\)
$$\displaystyle\frac{BD}{CD}=\frac{BM}{CN}\cdots ⑤$$
③より \(CE:AE=CN:AL\)
\(CE\cdot AL=AE\cdot CN\)
$$\displaystyle\frac{CE}{AE}=\frac{CN}{AL}\cdots ⑥$$
④, ⑤, ⑥ の辺々をかけると、
\(\displaystyle\frac{AF}{BF}\cdot\frac{BD}{CD}\cdot\frac{CE}{AE}\)
\(=\displaystyle\frac{AL}{BM}\cdot\frac{BM}{CN}\cdot\frac{CN}{AL}=1\)
よって、
$$\displaystyle\frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=1$$
メネラウスの定理の問題
三角形 \(ABC\) において、辺 \(AB\) 上と辺 \(AC\) の延長上にそれぞれ点 \(E\), \(F\) をとり、\(AE:EB=1:2\), \(AF:FC=3:1\) とする。直線 \(EF\) と直線 \(BC\) との交点を \(D\) とするとき、\(BD:DC\), \(ED:DF\) をそれぞれ求めよ。
>>詳細はこちらから
(解説)
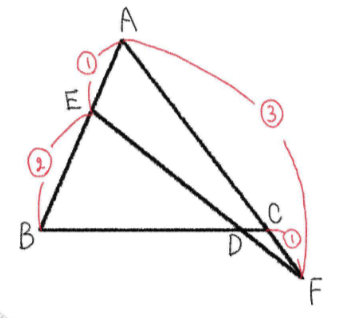
\(\triangle{ABC}\) と直線 \(EF\) について
図はこの角度で見る。
\(\displaystyle\frac{BE}{EA}\cdot\frac{AF}{FC}\cdot\frac{CD}{DB}=1\) より
\(\displaystyle\frac{2}{1}\cdot\frac{3}{1}\cdot\frac{CD}{DB}=1\)
\(2\cdot 3\cdot\frac{CD}{DB}=1\)
\(\displaystyle\frac{CD}{DB}=\frac{1}{6}\)
よって、\(BD:DC=6:1\)
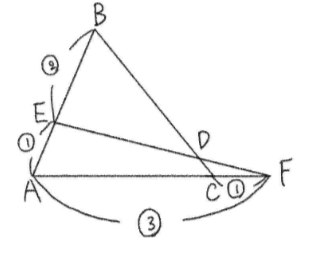
次に、\(\triangle{AEF}\) と直線 \(BC\) について
図はこの角度で見る。
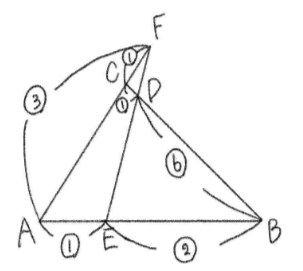
\(\displaystyle\frac{FC}{CA}\cdot \frac{AB}{BE}\cdot \frac{ED}{DF}=1\)
\(\displaystyle\frac{1}{2}\cdot \frac{3}{2}\cdot \frac{ED}{DF}=1\)
\(\displaystyle\frac{3}{4}\cdot \frac{ED}{DF}=1\)
\(\displaystyle\frac{ED}{DF}=\frac{4}{3}\)
よって、\(ED:DF=4:3\)
おわりに
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている学生の方
- 公務員試験の数学で困っている学生/社会人の方
- 統計学(統計検定)の勉強で困っている学生/社会人の方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
時間や料金などは相談して決められればと思っておりますが、塾に通うよりは高コスパかなと思います。また、基本的にはオンラインでの授業を想定していますが、場所によっては直接の指導が可能です。(プロフィール)
これまでは塾講師や高校で働いていたのですが、現在はデータサイエンティストとして活動しています。社会やビジネスで数学がどのように使われているのか、そういった話も交えながら進められればと思っております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。





質問や感想はコメントへ!