関数 \(f(x)\) が \(x=a\) で、
真 微分可能 \(\longrightarrow\) 連続
偽 連続 \(\longrightarrow\) 微分可能
関数 \(f(x)\) が微分可能であるとき、同時に連続であることが言えます。しかし、連続であっても同時に微分可能であるとは言えませんので注意が必要です！
微分係数と導関数
微分係数
① 定義 関数 \(f(x)\) の \(x=a\) における微分係数
\(f'(a)=\displaystyle\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}\)
\(a+h=x\) とおくと、
\(f’(a)=\displaystyle\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\)
② 微分可能と連続 関数 \(f(x)\) が \(x=a\) で微分可能ならば、\(f(x)\) は \(x=a\) である。ただし、逆は成り立たない。
解説
① の定義は数学Ⅱで学んだこととまったく同じである。
なお、関数 \(f(x)\) について、\(x=a\) における微分係数 \(f'(a)\) が存在するとき、\(f(x)\) は \(x=a\) で微分可能であるという。
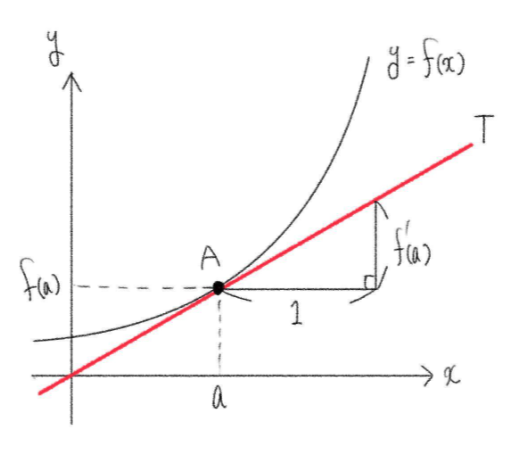
関数 \(y=f(x)\) が \(x=a\) で微分可能であるとき、曲線 \(y=f(x)\) 上の点 \(A(a\), \(f(a))\) における接線が存在し、微分係数 \(f'(a)\) は曲線 \(y=f(x)\) の点 \(A\) における接線 \(AT\) の傾きを表している。
「② 関数 \(f(x)\) が \(x=a\) で微分可能ならば、\(x=a\) で連続である。」の証明
\(\displaystyle\lim_{x\to a}\{f(x)-f(a)\}=\lim_{x\to a}\big\{\frac{f(x)-f(a)}{x-a}\cdot (x-a)\big\}=f'(a)\cdot 0=0\)
\(\displaystyle\lim_{x\to a}\{f(x)-f(a)\}\) について
最終的に、\(\displaystyle\lim_{x\to a} f(x)=f(a)\) を得るために、都合の良い形を持ってきただけです。
よって、\(\displaystyle\lim_{x\to a} f(x)=f(a)\)
ゆえに、\(f(x)\) は \(x=a\) で連続である。
なお、関数 \(f(x)\) が \(x=a\) で連続であっても、\(f(x)\) は \(x=a\) で微分可能とは限らないので、注意。
導関数
定義 関数 \(f(x)\) の導関数
\(f'(x)=\displaystyle\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}\)
解説
関数 \(f(x)\) が、ある区間のすべての \(x\) の値で微分可能であるとき、\(f(x)\) はその区間で微分可能であるという。
関数 \(f(x)\) がある区間で微分可能であるとき、その区間における \(x\) のおのおのの値 \(a\) に対して微分係数 \(f'(a)\) を対応させると、\(1\) つの新しい関数が得られる。
この新しい関数をもとの関数 \(f(x)\) の導関数といい、
記号 \(f'(x)\), \(y’\), \(\displaystyle\frac{dy}{dx}\), \(\displaystyle\frac{d}{dx} f(x)\)
などで表す。関数 \(y=f(x)\) からその導関数 \(f'(x)\) を求めることを、\(f(x)\) を微分するという。
また、\(x\) の増分 \(\Delta x\) に対する \(y=f(x)\) の増分 \(f(x+\Delta x)-f(x)\) を \(\Delta y\) で表すとき、関数 \(f(x)\) の導関数 \(f'(x)\) の定義の式は次のように表される。
\(f'(x)=\displaystyle\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\)
微分係数と導関数（問題）
次の関数は、[ ] で示された点において連続であるか、微分可能であるかを調べよ。
(1) \(f(x)=|x-a|\) (\(a\) は実数の定数) [\(x=a\)]
(2) \(f(x) =\begin{cases}\sin x & (x \geq 0)\\ x^2+x & (x < 0)\end{cases}\) [\(x=0\)]
解説
(1) \(f(x)=|x-a|\) (\(a\) は実数の定数) [\(x=a\)]
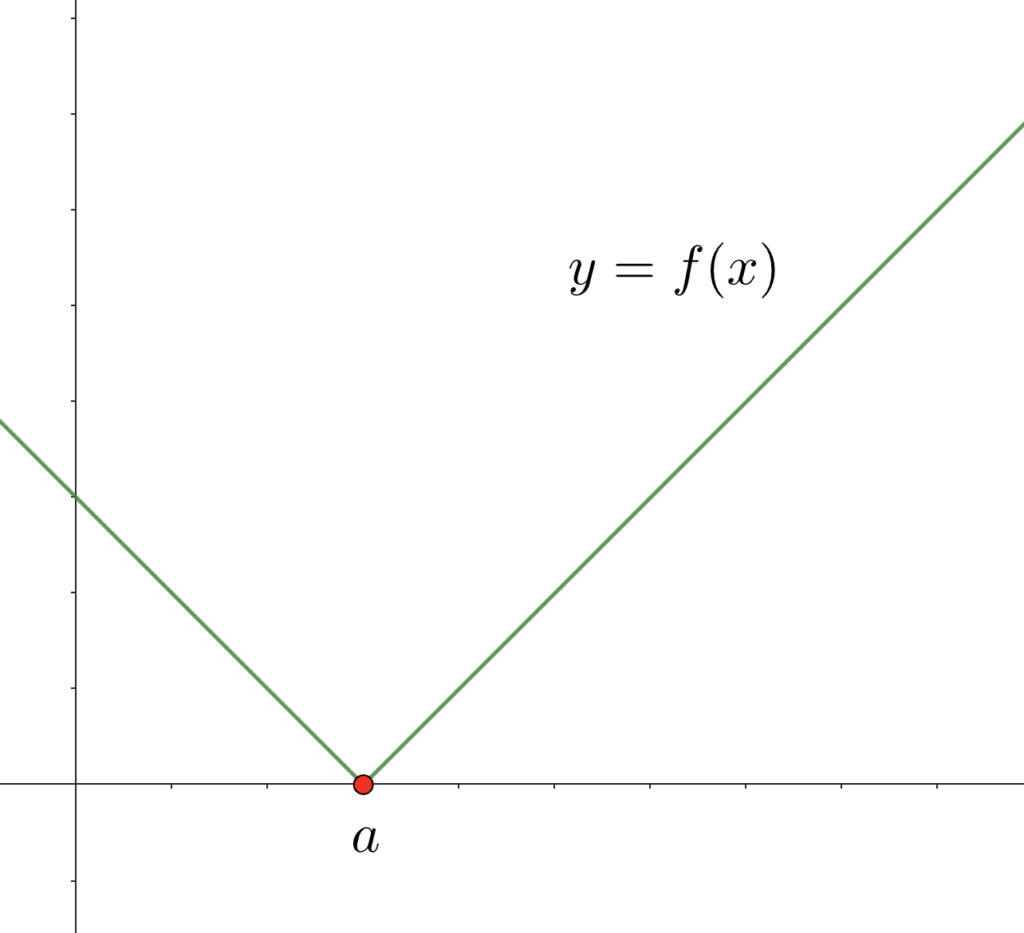
\(\displaystyle\lim_{x\to a+0} f(x)=\lim_{x\to a+0} (x-a)=0\)
\(\displaystyle\lim_{x\to a-0} f(x)=\lim_{x\to a+0} \{-(x-a)\}=0\)
ゆえに、\(\displaystyle\lim_{x\to a}f(x)=0\)
また、\(f(a)=0\) より \(\displaystyle\lim_{x\to a} f(x)=f(a)\)
よって、\(f(x)\) は \(x=a\) で連続である。
次に、
\(\displaystyle\lim_{h\to +0}\frac{f(a+h)-f(a)}{h}=\lim_{h\to +0}\frac{h-0}{h}=1\)
\(\displaystyle\lim_{h\to -0}\frac{f(a+h)-f(a)}{h}=\lim_{h\to -0}\frac{-h-0}{h}=-1\)
\(h\longrightarrow +0\) と \(h\longrightarrow -0\) のときの極限値が異なるから、\(f'(a)\) は存在しない。
すなわち、\(f(x)\) は \(x=a\) で微分可能ではない。
(2) \(f(x) =\begin{cases}\sin x & (x \geq 0)\\ x^2+x & (x < 0)\end{cases}\) [\(x=0\)]
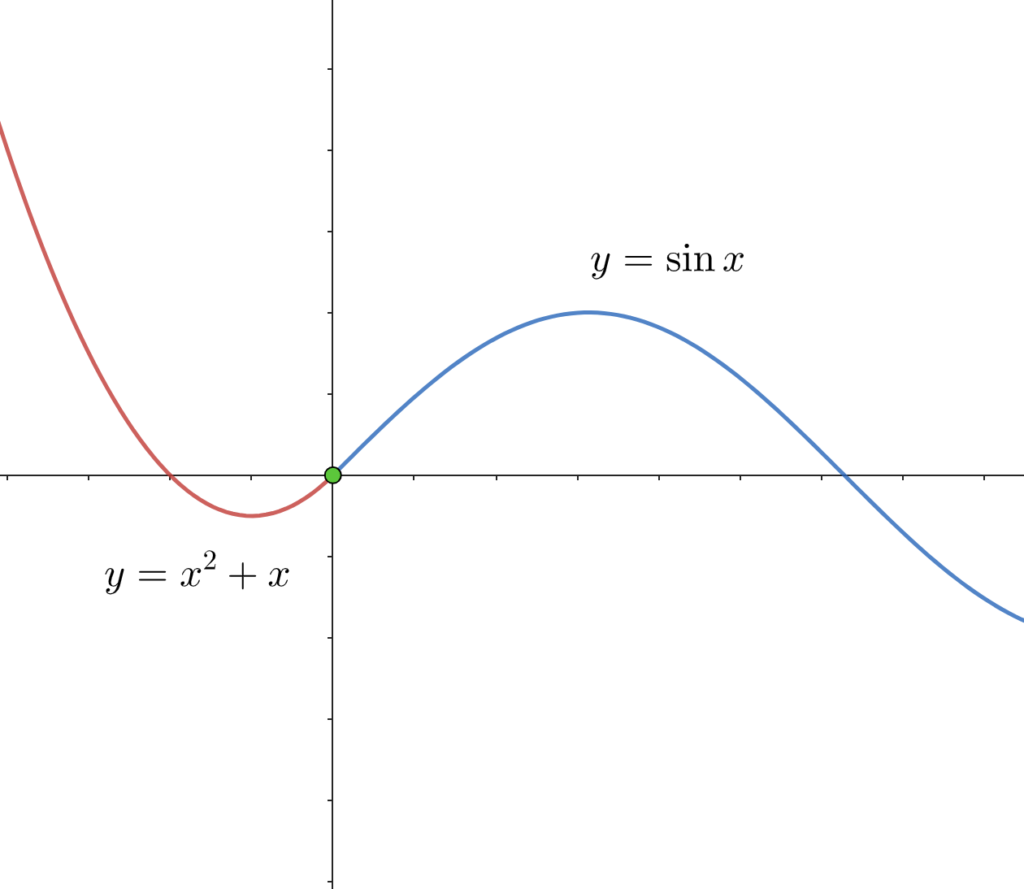
\(\displaystyle\lim_{h\to +0} \frac{f(0+h)-f(0)}{h}=\lim_{h\to +0}\frac{\sin h-0}{h}=\lim_{h\to +0}\frac{\sin h}{h}=1\)
\(\displaystyle\lim_{h\to -0} \frac{f(0+h)-f(0)}{h}=\lim_{h\to -0}\frac{(h^2+h)-0}{h}=\lim_{h\to -0}(h+1)=1\)
\(h\longrightarrow +0\) と \(h\longrightarrow -0\) のときの極限値が一致し、\(f'(0)=1\) となるので、\(f(x)\) は \(x=0\) で微分可能である。
したがって、\(f(x)\) は \(x=0\) で連続である。
おわりに
さいごまで記事を読んでいただきありがとうございました！
数学は、時間をかけて勉強すれば誰でも成績を上げられます！
しかし、時間には限りがあります。
アプリや塾/家庭講師など自分に合ったサポートを取り入れることで、限りある時間を効率的に使うことができます。
▼自走して学習が進められる人
日々の悩みを解決できるコーチング面談や日々の学習計画を見直せるサポートがおすすめです。
▼自走して学習が進められない人
毎週講師による授業をしっかり受けて、宿題を設定してもらうサポートがおすすめです。
コメントはお気軽に♪