最短経路の組合せ
今回は最短経路を求める問題です。下の図のように、
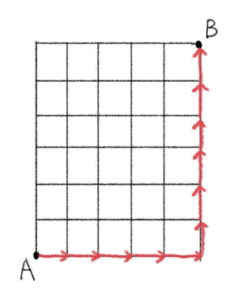
\(A\) から、右に \(5\) 回、上に \(6\) 回進むと \(B\) にたどり着くので、\(A\) から \(B\) までの進み方は、
→→→→→↑↑↑↑↑↑
の並び方の場合の数と一致する。
最短経路（問題）
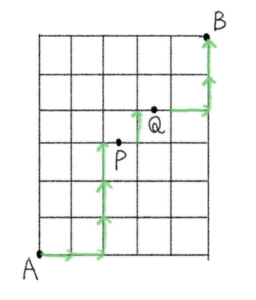
下の図のように、道路が碁盤の目のようになった街がある。地点 \(A\) から地点 \(B\) までの長さが最短の道を行く時、次の場合は何通りの道順があるか。
(1) 全部の道順
(2) 地点 \(C\) を通る
(3) 地点 \(P\) は通らない
(4) 地点 \(P\) も地点 \(Q\) も通らない
＞＞詳細はこちらから
最短経路（解説）
(1) 全部の道順
\(A\) から、右に \(5\) 回、上に \(6\) 回進むと \(B\) にたどり着くので、\(A\) から \(B\) までの進み方は →→→→→↑↑↑↑↑↑の並び方の場合の数と一致する。
\({}_{11}C_5=\displaystyle\frac{{}_{11}P_5}{5!}\)
\(=\displaystyle\frac{11\times 10\times 9\times 8\times 7}{5\times 4\times 3\times 2\times 1}=462\)
(2) 地点 \(C\) を通る
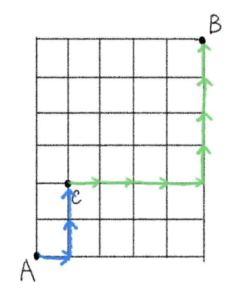
\(A\) から\(C\) までの進み方
\({}_3C_1=3\)
\(C\) から \(B\) までの進み方
\({}_8C_4=\displaystyle\frac{{}_8P_4}{4i}\)
\(=\displaystyle\frac{8\times 7\times 6\times 5}{4\times 3\times 2\times 1}=70\)
よって、\(3\times 70=210\)
(3) 地点 \(P\) は通らない
（全体）\(-\)（\(P\) を通る）
地点 \(P\) を通る。
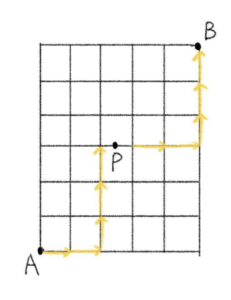
\({}_5C_2=\displaystyle\frac{{}_5P_2}{2i}=10\)
\({}_5C_2=\displaystyle\frac{{}_5P_2}{2i}=10\)
よって、\(10\times 10=100\)
したがって、\(462-100=362\)
(4) 地点 \(P\) も地点 \(Q\) も通らない
（全体）\(-\)（（\(P\) を通る）\(+\)（\(Q\) を通る）\(-\)（\(P\) と \(Q\) を通る））
全体
(1) より \(462\) 通り
\(P\) を通る
\({}_5C_2\times {}_5C_2=10\times 10=100\) 通り
\(Q\) を通る
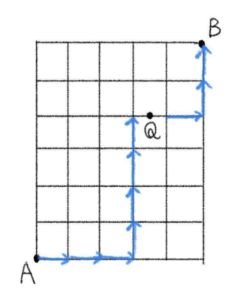
\({}_7C_3\times {}_3C_1=35\times 3=105\) 通り
\(P\) と \(Q\) を通る
\({}_5C_2\times {}_3C_1=10\times 3=30\) 通り
よって、\(462-(100+105-30)=287\)
おわりに
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！