\(y=x\sin x\) のグラフ
今回は、\(y=x\sin x\) のグラフを解説します。
ほとんどのグラフは、微分法を使用し増減を調べることによって描くことができます。しかし、今回の式は微分法だけでは手がかりが少なくグラフを描くことができません。特殊な考え方をするので入試本番で突然出てきて焦ることのないように対策しておきましょう。
サインのグラフ
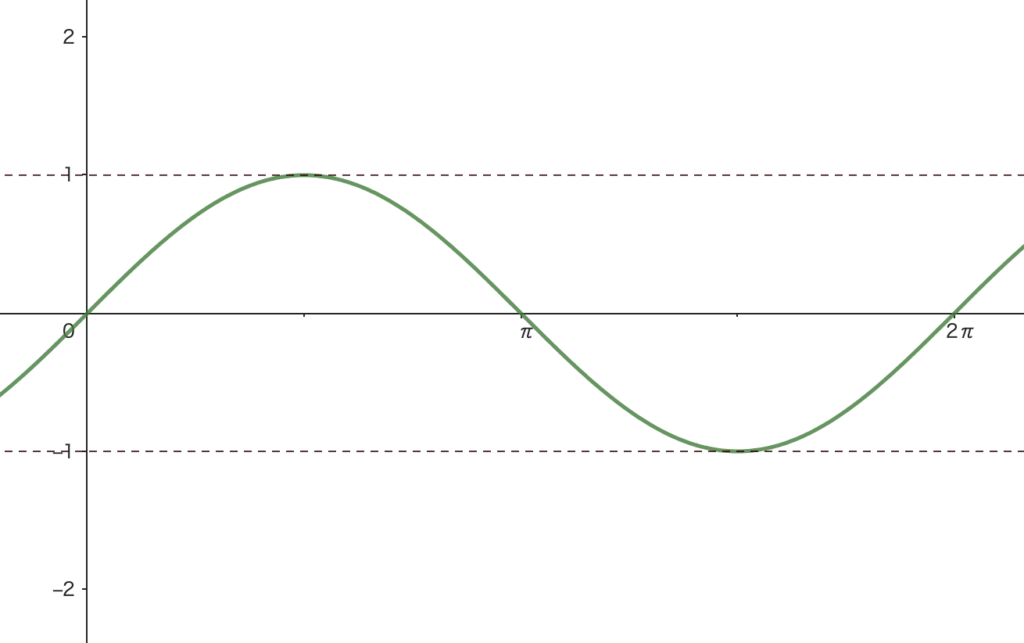
\(y=\sin\theta\) のグラフ
① \(-1\leq \theta \leq 1\)
② \(x=0\), \(\pi\), \(2\pi\), \(\cdots\) のとき、\(y=0\)
③ \(x=\frac{1}{2}\pi\), \(\frac{5}{2}\pi\), \(\cdots\) のとき、\(y=1\)
④ \(x=\frac{3}{2}\pi\), \(\frac{7}{2}\pi\), \(\cdots\) のとき、\(y=-1\)
以上のことに気をつけて、グラフを描くと、
微分法を用いたグラフの描き方
\(y=f(x)\) のグラフ
① \(f'(x)\)（導関数）を求める。
② \(f'(x)=0\) のときの \(x\) を計算する。
③ 増減表を書く。
④ 増減表をもとにグラフを描く。
\(f'(a)\) は \(x=a\) における接線の傾きを表します。接戦の傾き具合によってグラフを描いていくのが、微分法を用いたグラフの描き方です。
問題
\(f(x)=x\sin x\) のグラフを描きなさい。
＞＞詳細はこちらから
解説
\(f'(x)=\sin x+x\cos x\) となり、\(f'(x)=0\) を考えると、
$$\sin x+x\cos x=0$$
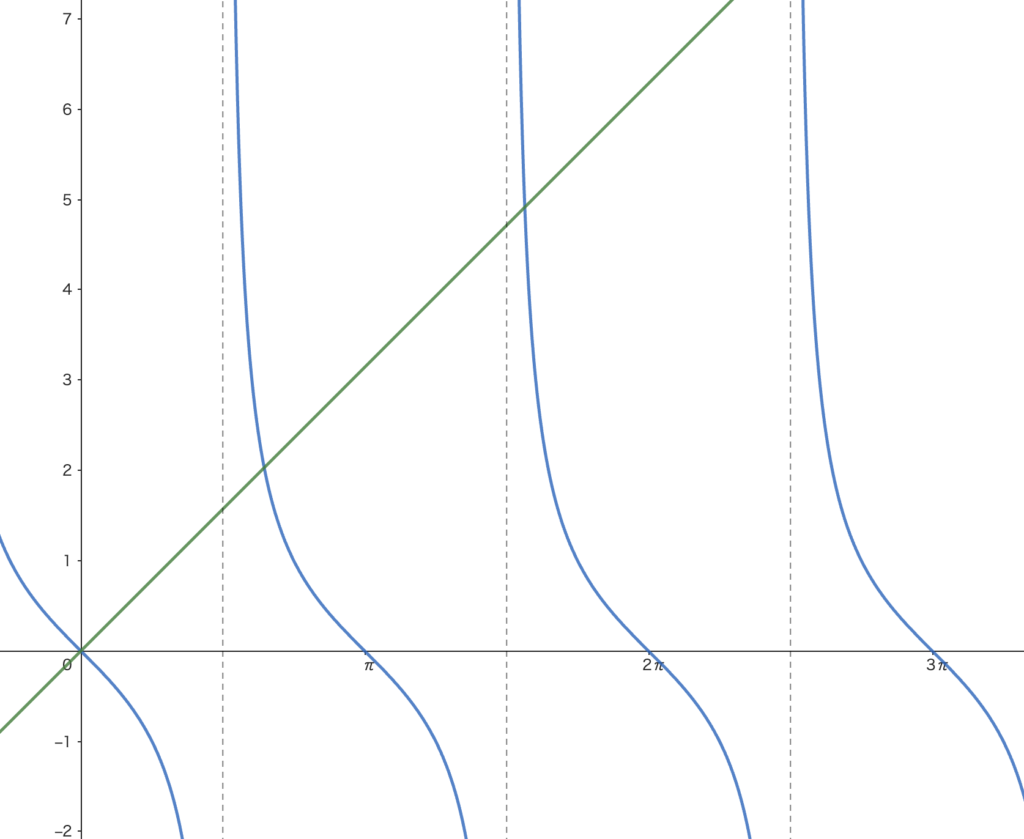
\begin{eqnarray} x\cos x &=& -\sin x\\ x &=& -\displaystyle\frac{\sin x}{\cos x}\\ x &=& -\tan x \end{eqnarray}\(g(x)=x\) と \(g(x)=-\tan x\) とおくと、\(x=\displaystyle\frac{\pi}{2}+n\pi\) (\(n=1,2,3\cdots\))
\(n\) を大きくするほど近づきますが、厳密に与えられる極値は \(x=0\) のみです。
次に、原点を通る接線を考えます。接点 \((a\), \(a\sin a)\) とおくと、
$$y-a\sin a=f'(x)(x-a)$$
原点を通るので、
$$0-a\sin a=(\sin a+a\cos a)(-a)$$
\(0=-a^2\cos a\) となり、接点は \(a=0\), \(a=\displaystyle\frac{\pi}{2}+n\pi\)
よって、\(n\) が偶数の時は \(y=x\)、\(n\) が奇数の時は \(y=-x\) が接線となる。
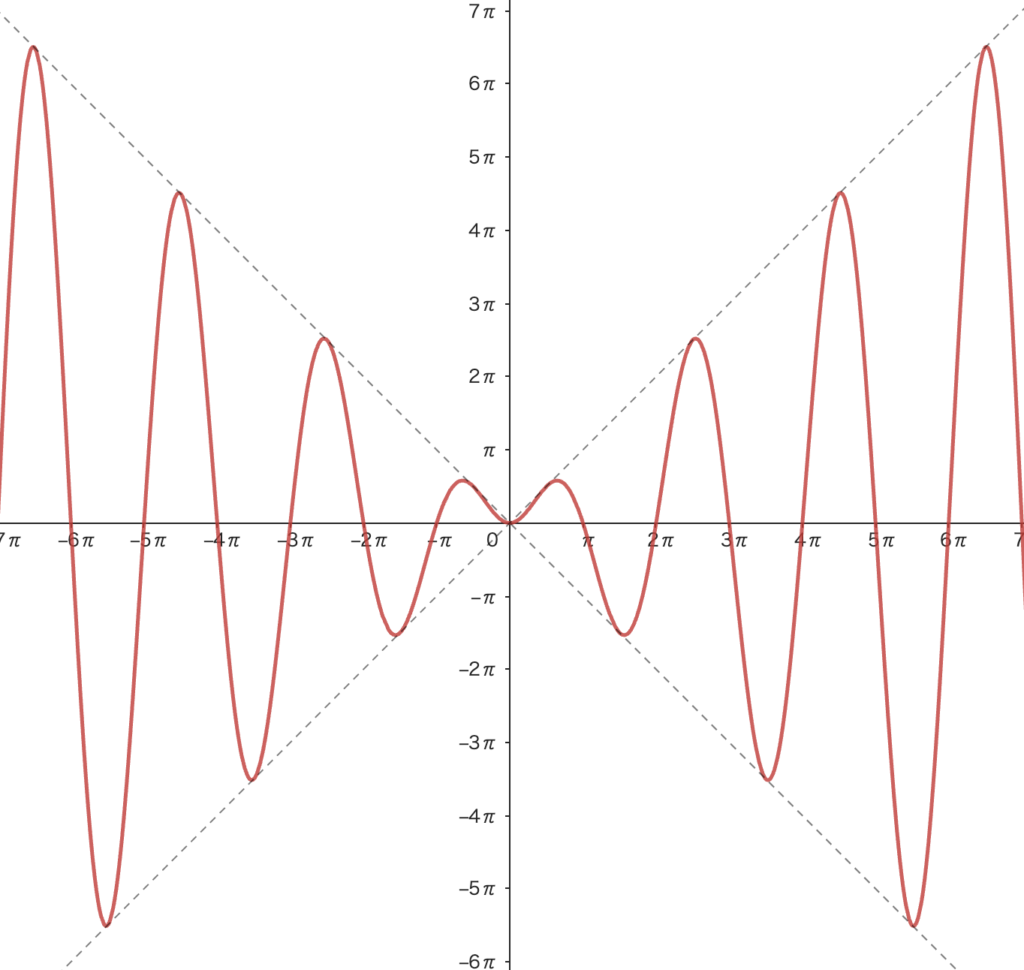
また、\(f(x)=x\sin x\) において、
\begin{eqnarray} f(\frac{\pi}{2}) &=& \frac{\pi}{2}\\ f(\frac{3}{2}\pi)&=& -\frac{3}{2}\pi\\ f(\frac{5}{2}\pi)&=& \frac{5}{2}\pi\cdots \end{eqnarray}であることに気をつけると、(負の方向も同様に考える。)
おわりに
今回は、微分法では増減が見えてこない関数のグラフを描いてみました。
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！