曲線の凹凸・変曲点
今回は変曲点についてです！
変曲点とは、「グラフの曲がり方が変わる点」のことです。
言い換えると、「接線の傾きが増加から減少に切り替わる点」とも言えます！
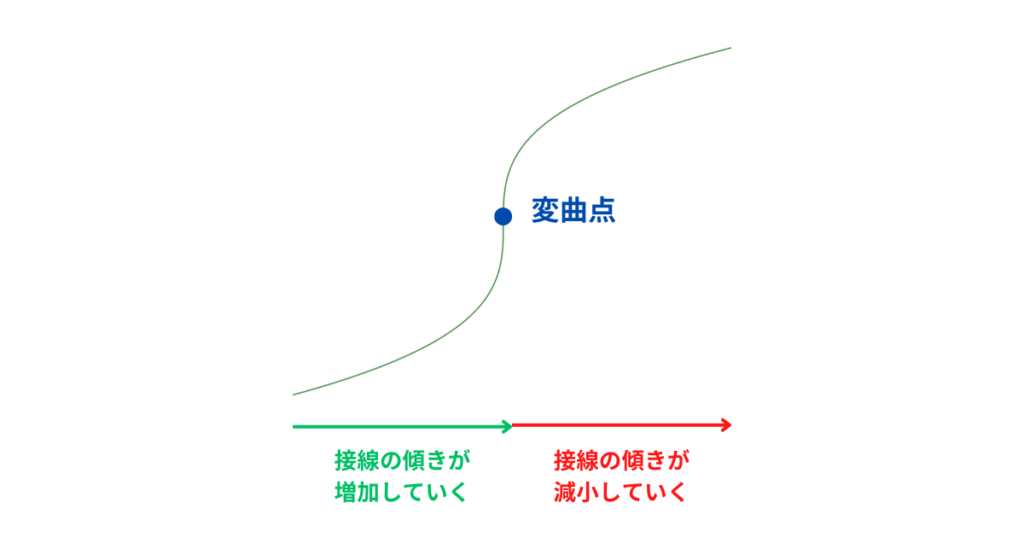
[1] 曲線の凹凸
関数 \(f(x)\) は第 \(2\) 次導関数 \(f”(x)\) をもつとする。
\(f”(x)>0\) である区間では、曲線 \(y=f(x)\) は下に凸
\(f”(x)<0\) である区間では、曲線 \(y=f(x)\) は上に凸
[2] 変曲点
① 凹凸が変わる曲線上の点のこと。\(f”(a)=0\) であって、\(x=a\) の前後で \(f”(x)\) の符号が変わるならば、点 \(P(a\), \(f(a))\) は曲線 \(y=f(x)\) の変曲点である。
② 点 \((a\), \(f(a))\) が曲線 \(y=f(x)\) の変曲点ならば \(f”(a)=0\)
関数のグラフの概形
次の ① 〜 ⑥ に注意してかく。
① 定義域
\(x\), \(y\) の変域に注意して、グラフの存在範囲を調べる。
② 対称性
\(x\) 軸対称、\(y\) 軸対称、原点対称などの対称性を調べる。
③ 増減と極値
\(y’\) の符号の変化を調べる。
④ 凹凸と変曲点
\(y”\) の符号の変化を調べる。
⑤ 座標軸との共有点
\(x=0\) のときの \(y\) の値、\(y=0\) のときの \(x\) の値を求める。
⑥ 漸近線
\(x\longrightarrow\pm\infty\) のときの \(y\) の極限や、\(y\longrightarrow\pm\infty\) となる \(x\) の値を調べる。
第 \(2\) 次導関数と極値
\(x=a\) を含むある区間で \(f”(x)\) は連続であるとする。
① \(f'(a)=0\), \(f”(a)<0\) ならば、\(f(a)\) は極大値である。
② \(f'(a)=0\), \(f”(a)>0\) ならば、\(f(a)\) は極小値である。
関数のグラフ（問題）
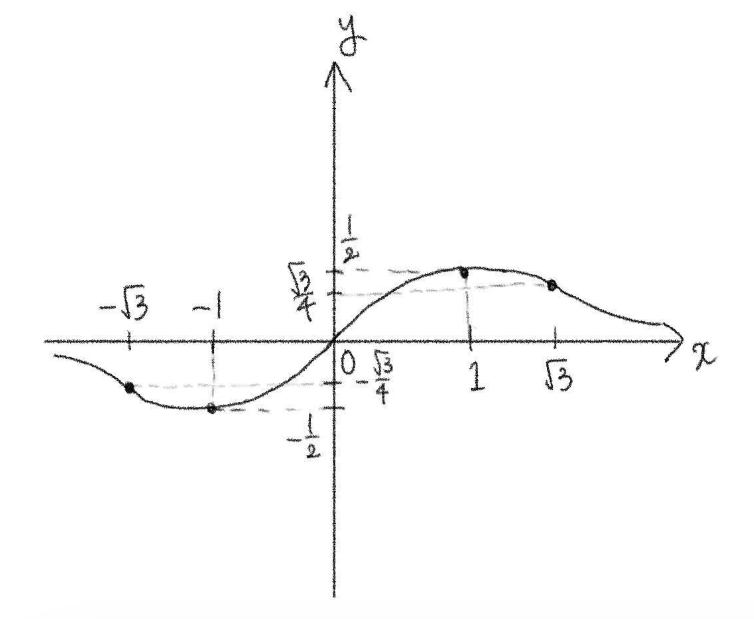
曲線 \(y=\displaystyle\frac{x}{x^2+1}\) の変曲点を求め、グラフを描きなさい。
＞＞詳細はこちらから
関数のグラフ（解説）
\(y’=\displaystyle\frac{x’\cdot (x^2+1)-x\cdot (x^2+1)’}{(x^2+1)^2}\)
\(=\displaystyle\frac{x^2+1-x\cdot 2x}{(x^2+1)^2}\)
\(=-\displaystyle\frac{x^2-1}{(x^2+1)^2}\)
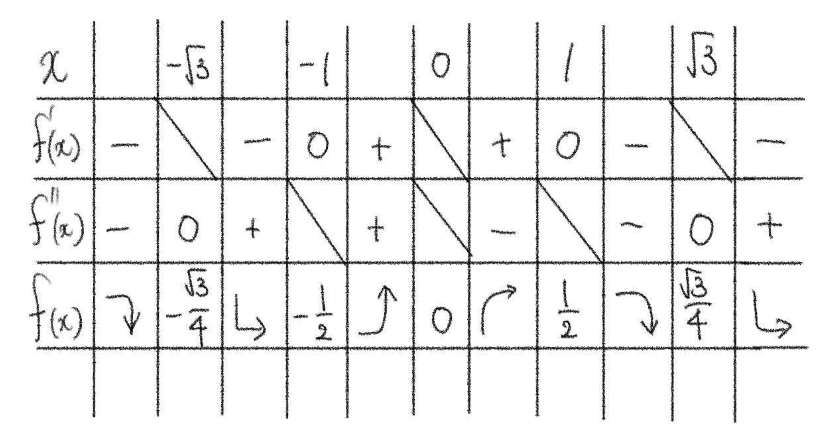
\(y’=0\) とすると \(x=1\), \(-1\)
\(y”=-\displaystyle\frac{(x^2-1)'(x^2+1)^2-(x^2-1)\{(x^2+1)^2\}’}{(x^2+1)^4}\)
\(=-\displaystyle\frac{2x(x^2+1)^2-(x^2-1)\cdot 2(x^2+1)\cdot 2x}{(x^2+1)^4}\)
\(=-\displaystyle\frac{2x(x^2+1)^2-4x(x^2-1)(x^2+1)}{(x^2+1)^4}\)
\(=-\displaystyle\frac{2x(x^2+1)\{(x^2+1)-2(x^2-1)\}}{(x^2+1)^4}\)
\(=-\displaystyle\frac{2x(x^2+1)(-x^2+3)}{(x^2+1)^4}\)
\(=\displaystyle\frac{2x(x^2-3)}{(x^2+1)^3}\)
\(=\displaystyle\frac{2x(x+\sqrt{3})(x-\sqrt{3})}{(x^2+1)^3}\)
\(y”=0\) とすると \(x=0\), \(\pm\sqrt{3}\)
\(y”\) の符号を調べると、常に \((x^2+1)^3>0\) であるから、この曲線の凹凸は次の表のようになる。
おわりに
さいごまで読んでいただきありがとうございました！
【最新】こちらの記事がおすすめ！