小学5年生で初めて扱うのが円周率です。
小学校の算数では「円周率 \(=3.14\)」という数字を暗記していれば大体の問題を解くことができます。
しかし、ただ数字を暗記するのではなく、「円周率とは何なのか」といった根本的な部分や円周率の求め方を知っていると算数の勉強がより楽しくなるでしょう。
円周率とは?
円周率は、
「(円周の長さ)\(\div\)(直径の長さ)」
で求められます。
円周率は「円の直径と円周の長さの比」というように定義されます。
円周率が \(3.14\) という決まった数で表されることからもわかるように、どのような大きさの円でも「円周は直径の何倍か」に対する答えはいつも同じ数字となります。
円周率を求める公式はさまざまな問題で活用できるので、しっかり覚えておきましょう。
円周率の近似値を求めてみよう
円周率は近い値を求めようとすればするほど計算が大変になりますが、今回は正十二角形を用いて近似値を求めてみようと思います。
半径 \(1\) の円に内接するように正十二角形を、外接するように正十二角形を描く。
STEP1 内接する正十二角形の1辺を求める
半径が \(1\) より内接する正十二角形の \(1\) 辺の長さを \(\ell\) とおくと、
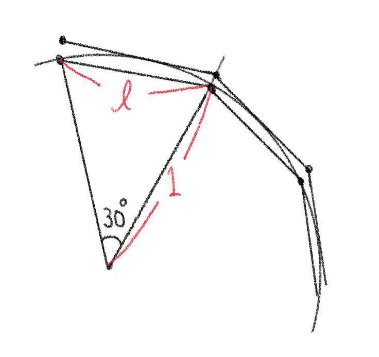
\(\ell^2=1^2+1^2-2\cdot 1\cdot 1\cdot\cos30^{\circ}\)
\(=2-2\cdot\frac{\sqrt{3}}{2}\)
\(=2-\sqrt{3}\)
\(\ell=\sqrt{2-\sqrt{3}}\)
STEP2 中心から外接する正十二角形の頂点までの距離を求める
また、中心から外接する正十二角形の頂点までの距離を \(R\) とおくと、
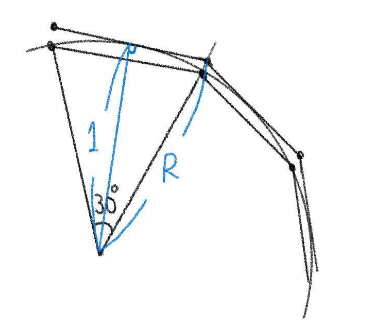
図より、\(\cos\left(\displaystyle\frac{30}{2}\right)^\circ=\displaystyle\frac{1}{R}\)
半角の公式より
\(\cos^2\left(\displaystyle\frac{30}{2}\right)^{\circ}=\displaystyle\frac{1+\cos 30^{\circ}}{2}\)
\(=\displaystyle\frac{1+\frac{\sqrt{3}}{2}}{2}\)
\(=\displaystyle\frac{2+\sqrt{3}}{4}\)
\(\cos\left(\displaystyle\frac{30}{2}\right)^{\circ}=\displaystyle\frac{\sqrt{2+\sqrt{3}}}{2}\)
よって、\(\displaystyle\frac{\sqrt{2+\sqrt{3}}}{2}=\frac{1}{R}\)
\(R=\displaystyle\frac{2}{\sqrt{2+\sqrt{3}}}\)
STEP3 外接する正十二角形の1辺を求める
したがって、外接する正十二角形の \(1\) 辺の長さ \(m\) は、
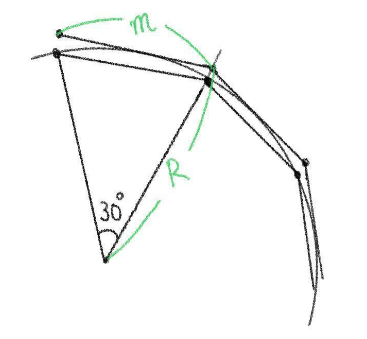
\(m^2=\left(\displaystyle\frac{2}{\sqrt{2+\sqrt{3}}}\right)^2+\left(\displaystyle\frac{2}{\sqrt{2+\sqrt{3}}}\right)^2-2\cdot\left(\displaystyle\frac{2}{\sqrt{2+\sqrt{3}}}\right)^2\cdot \displaystyle\frac{\sqrt{3}}{2}\)
\(=\displaystyle\frac{4}{2+\sqrt{3}}+\displaystyle\frac{4}{2+\sqrt{3}}-2\cdot\displaystyle\frac{4}{2+\sqrt{3}}\cdot \frac{\sqrt{3}}{2}\)
\(=\displaystyle\frac{8}{2+\sqrt{3}}-\cdot\displaystyle\frac{4\sqrt{3}}{2+\sqrt{3}}\)
\(=4\cdot\displaystyle\frac{2-\sqrt{3}}{2+\sqrt{3}}\)
\(=4(2-\sqrt{3})^2\)
\(m=2(2-\sqrt{3})\)
STEP4 円周率の近似値を求める
ここで、
(内接する正十二角形の外周) \(<\) 円周 \(<\) (外接する正十二角形の外周) より
\(12\times \sqrt{2-\sqrt{3}}\)
\(<2\cdot\) 円周率
\(<12\times 2(2-\sqrt{3})\)
\(6\sqrt{2-\sqrt{3}}<\) 円周率 \(<12(2-\sqrt{3})\)
\(\sqrt{3}=1.73\) として計算する。
\(12(2-\sqrt{3})=12\times 0.27=3.24\)
\(6\sqrt{2-\sqrt{3}}=6\times\sqrt{0.27}=6\times\sqrt{\displaystyle\frac{27}{100}}\)
\(=6\times\sqrt{\displaystyle\frac{3\sqrt{3}}{10}}=\displaystyle\frac{9}{5}\times\sqrt{3}\)
\(=1.8\times 1.73=3.114\)
よって、
\(3.114<\) 円周率 \(<3.24\)
であることがわかります。今回使用した正十二角形の角数を増やせばより円周率に近い値を取ることができます。
おわりに
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている学生の方
- 公務員試験の数学で困っている学生/社会人の方
- 統計学(統計検定)の勉強で困っている学生/社会人の方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
時間や料金などは相談して決められればと思っておりますが、塾に通うよりは高コスパかなと思います。また、基本的にはオンラインでの授業を想定していますが、場所によっては直接の指導が可能です。(プロフィール)
これまでは塾講師や高校で働いていたのですが、現在はデータサイエンティストとして活動しています。社会やビジネスで数学がどのように使われているのか、そういった話も交えながら進められればと思っております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。




質問や感想はコメントへ!