対数関数のグラフと性質
対数関数 \(y=\log_a x\) のグラフや性質について解説していきます。
\(a\):底
\(x\):真数
対数関数のグラフの形と性質まとめ
対数関数 \(y=\log_a x\) のグラフの形は、底の値によって異なり、\(2\) パターンに分けられます。
\(y=\log_2 x\) を例にグラフを描いてみます。
\(a>1\)
底が \(1\) より大きい場合は、\(x\) の値が増加するにつれて、\(y\) はなめらかに増加していくようなグラフになります。
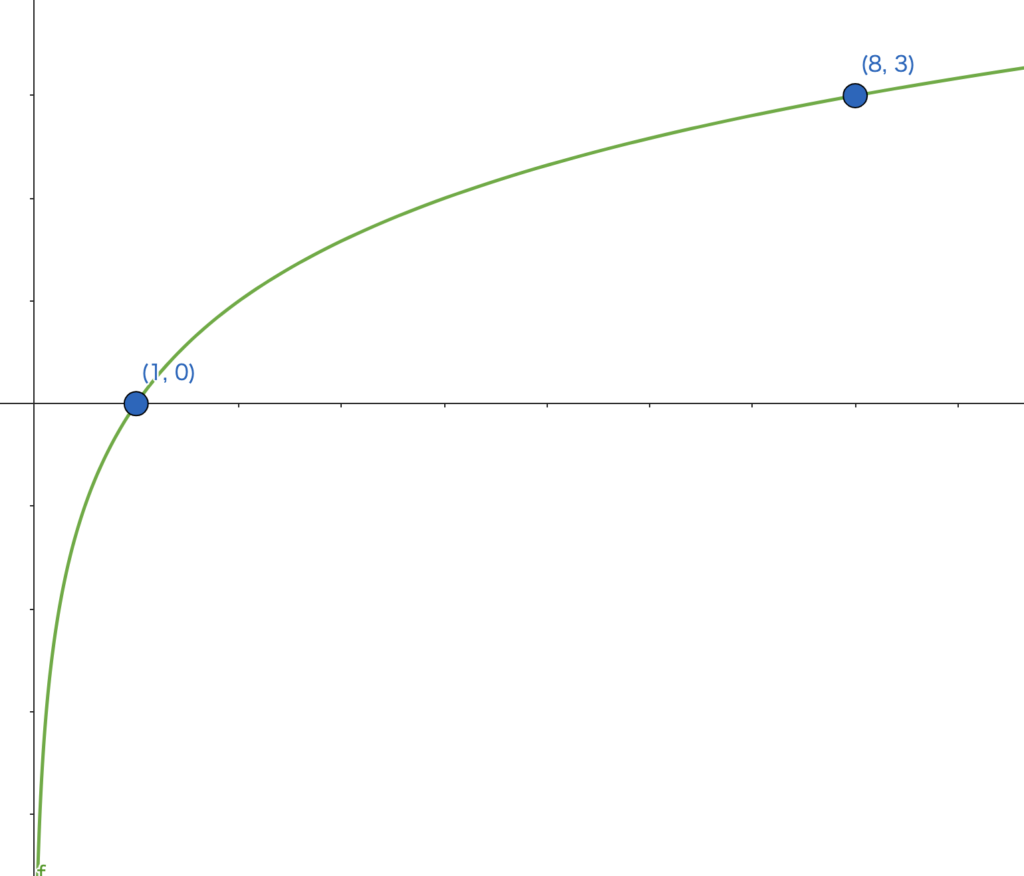
\(0<a<1\)
底が \(0\) と \(1\) の間のとき(分数のとき)、\(x\) の値が増加するにつれて、\(y\) はなめらかに減少していくようなグラフになります。
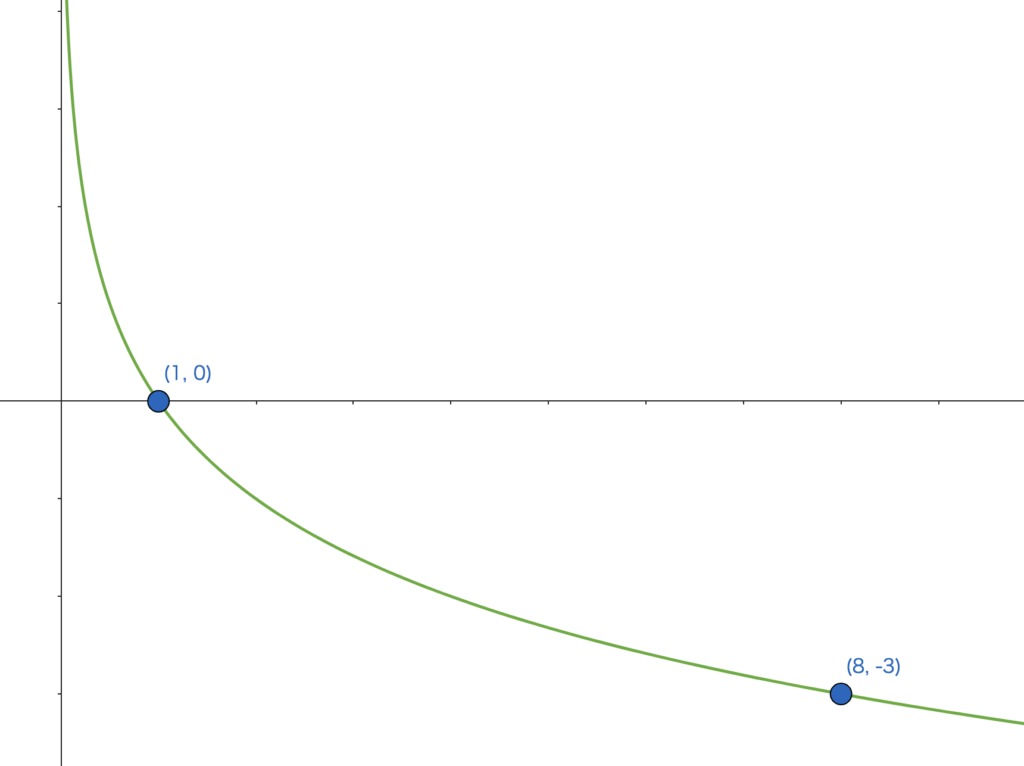
指数関数と対数関数
対数関数 \(y=\log_a x\) のグラフは、指数関数 \(y=a^x\) のグラフと \(y=x\) に関して対称になります。
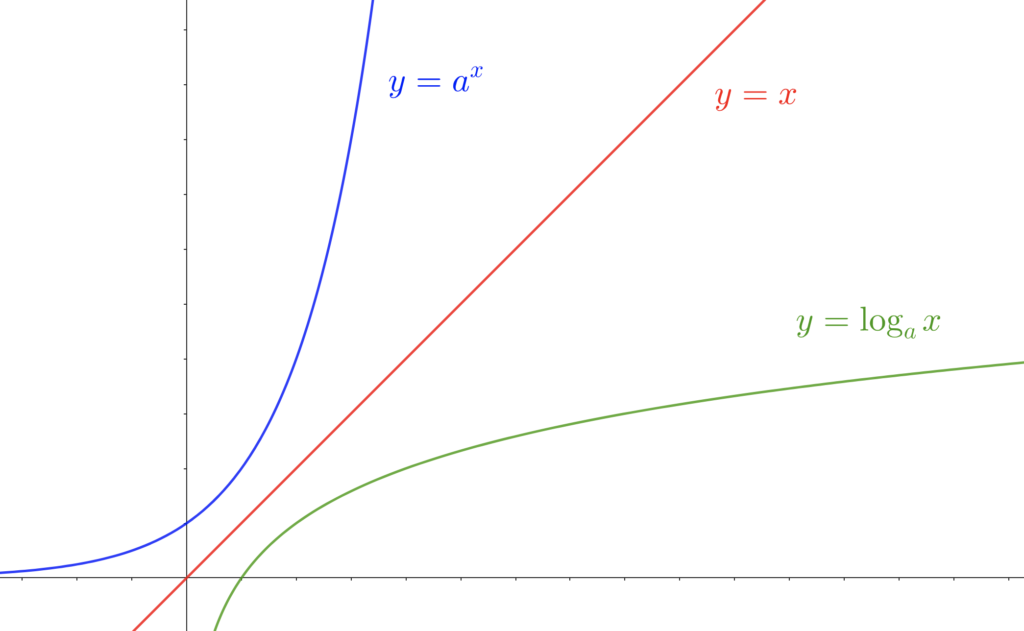
\(y=\log_2 x\) のグラフを例に考えます。
対数の定義より
\(y=\log_2 x\) \(\longleftrightarrow\) \(x=2^y\)
ここで、\(x=2^y\) と指数関数 \(y=2^x\) は、\(x\) と \(y\) が入れ替わったものです。
よって、点 \(P\) \((a\), \(b)\) が \(y=2^x\) のグラフ上にあるとき、点 \(Q\) \((b\), \(a)\) は \(y=\log_2 x\) のグラフ上にあります。
\(2\) 点 \(P\), \(Q\) は直線 \(y=x\) に関して対称であるから、\(y=\log_2 x\) のグラフと \(y=2^x\) のグラフは直線 \(y=x\) に関して対称となります。
対数関数のグラフの書き方
対数関数のグラフの書き方は、次の手順でかいていきます。
対数関数 \(y=\log_a x\) のグラフをかく手順
STEP ① 点 \(1\), \(0)\) を打つ。
STEP ② 点 \((a\), \(1)\) を打つ。
STEP ③ \(y\) 軸をグラフの漸近線として、①・②の点を通る曲線をかく。
この手順で、\(y=\log_3 x\) のグラフをかいてみましょう。
STEP ①
まずは点 \((1\), \(0)\) に点を打ちます。
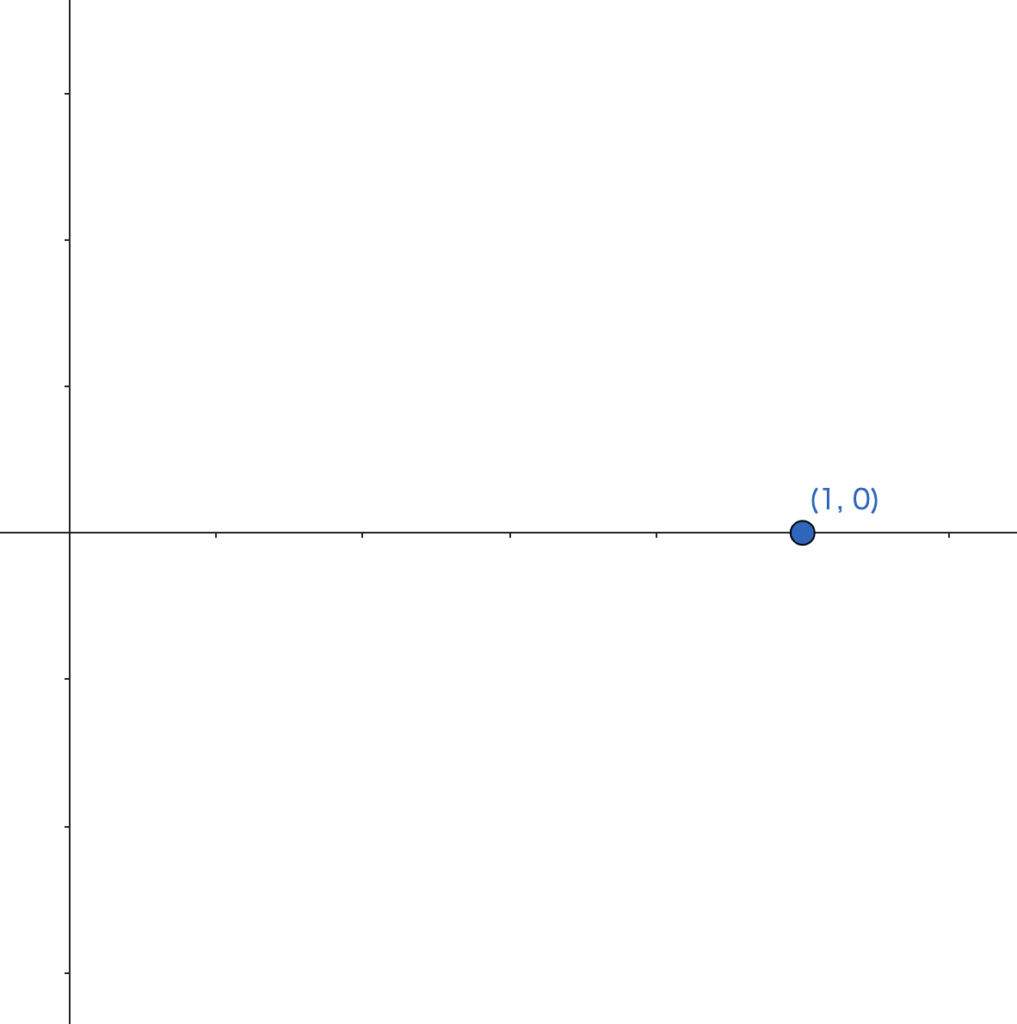
STEP ②
\(y=\log_3 x\) の底は \(3\) で、\(x=3\) のとき \(y=1\) となるので、点 \((3\), \(1)\) を通ります。この点を打ちます。
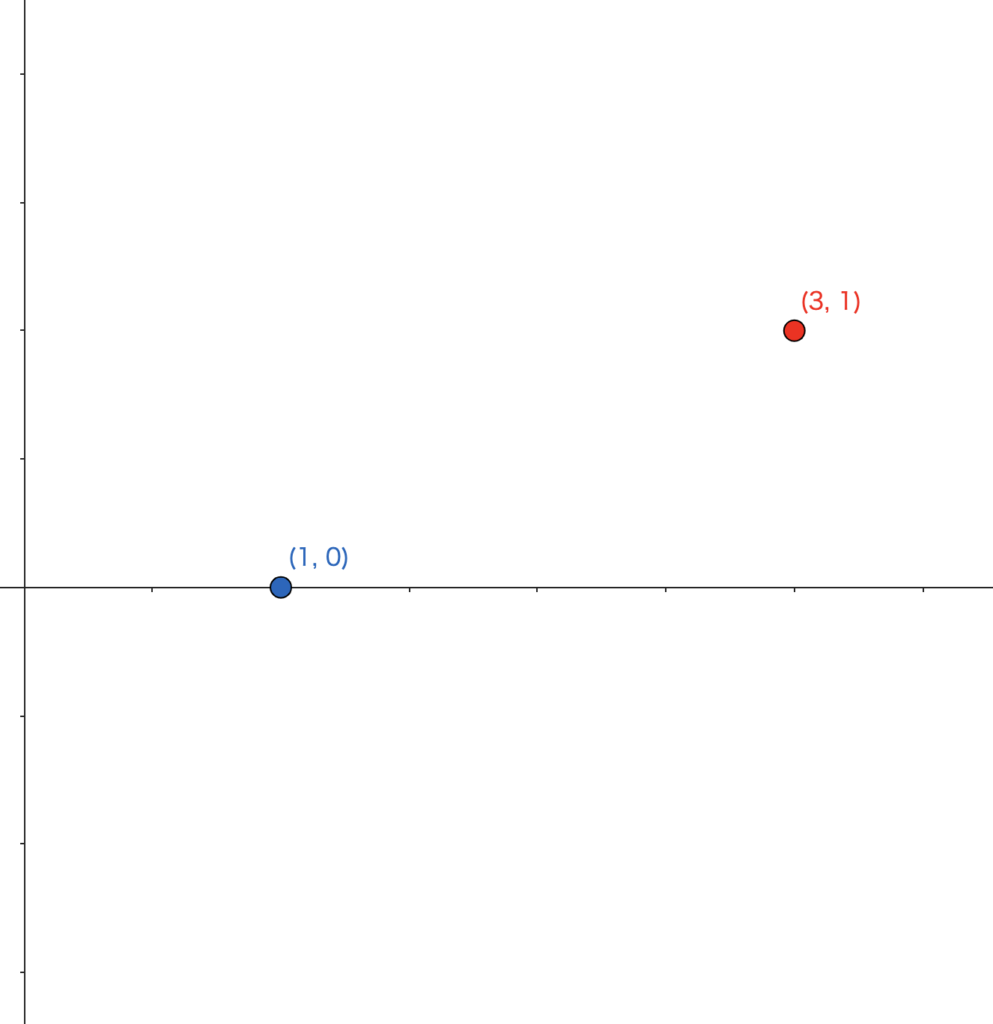
STEP ③
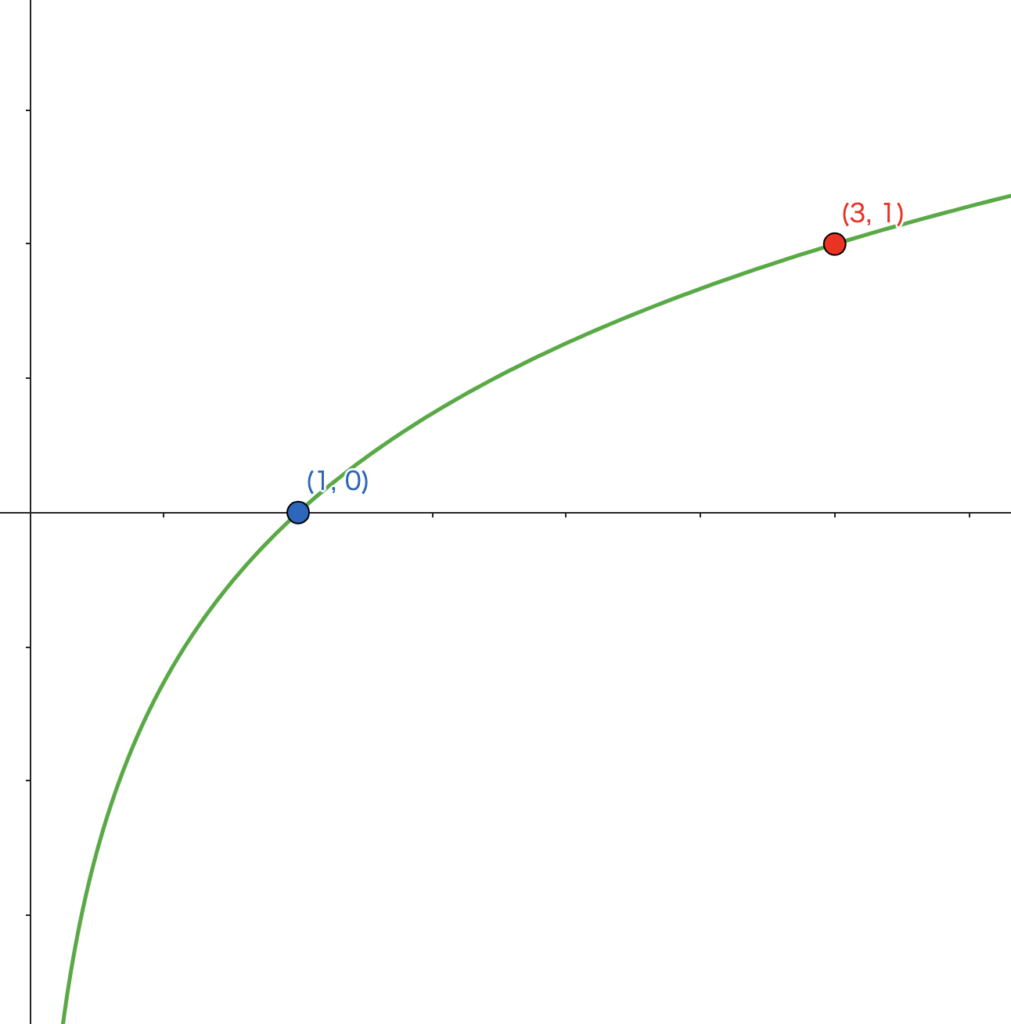
さいごに、\(y\) 軸を漸近線として、①・②の \(2\) 点を通るなめらかな曲線をかきます。このかき方の要領は、\(2\) 次関数のグラフと同じです。
対数関数のグラフの平行移動・対称移動
>>詳細はこちらから
対数関数のグラフの平行移動・対称移動まとめ
\(y=\log_a x\) のグラフの平行移動・対称移動は次のようになります。
\(y=\log_a x\) のグラフの平行移動・対称移動
・\(x\) 軸方向に \(p\), \(y\) 軸方向に \(q\) だけ平行移動
→\(y=\log_a (x-p)+q\)
・\(x\) 軸に関して対称移動
→\(y=-\log_a x=\log_{\frac{1}{2}} x\)
・\(y\) 軸に関して対称移動
→\(y=\log_a (-x)\)
・原点に関して対称移動
→\(y=-\log_a (-x)=\log_{\frac{1}{a}} (-x)\)
考え方は \(y=f(x)\) のグラフの平行移動・対称移動と同様です。
対数関数のグラフの平行移動・対称移動の問題
次の関数のグラフをかけ。また、関数 \(y=\log_2 x\) のグラフとの位置関係を述べよ。
(1) \(y=\log_2 (x+1)\)
(2) \(y=\log_{\frac{1}{2}} x\)
(3) \(y=\log_2 (2x-4)\)
解答
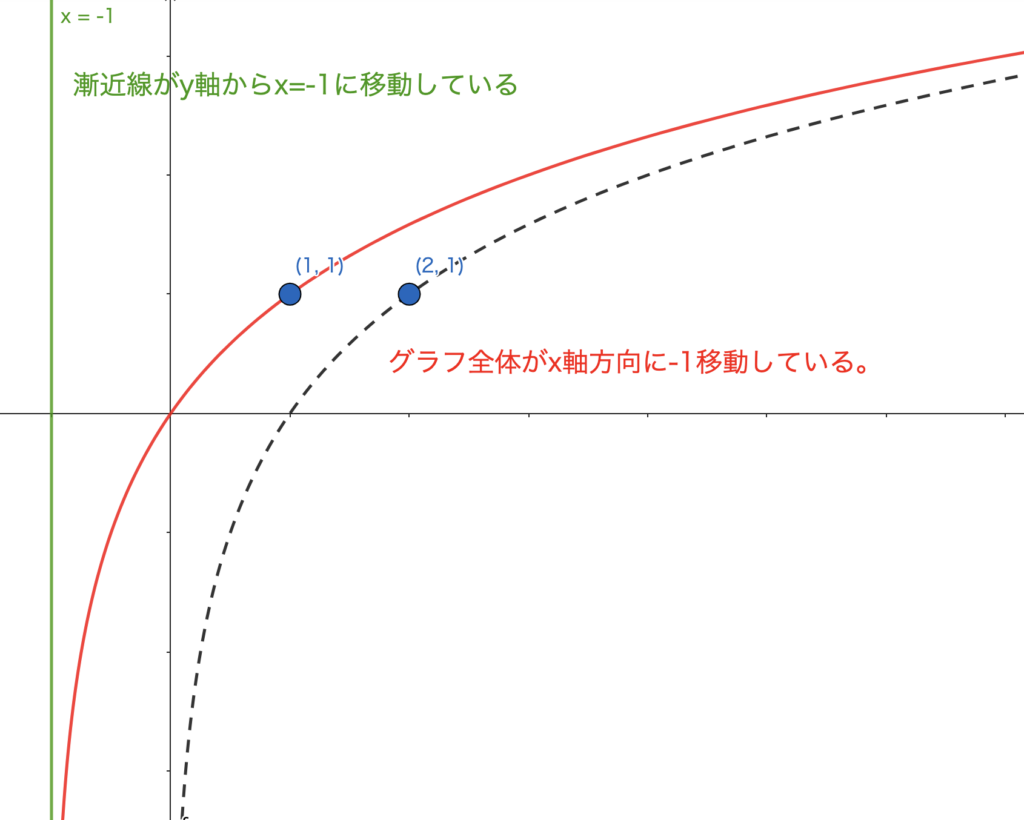
(1) \(y=\log_2 (x+1)=\log_2{x-(-1)}\)
したがって、\(y=\log_2 (x+1)\) のグラフ(赤線)は、
\(y=\log_2 x\) のグラフ(点線)を \(x\) 軸方向に \(-1\) だけ平行移動したもの。
(2) 底の変換公式を利用して、底を \(2\) にします。
\(y=\log_{\frac{1}{2}} x=\displaystyle\frac{\log_2 x}{\log_2 {\frac{1}{2}}}\)
\(=\displaystyle\frac{\log_2 x}{\log_2 2^{-1}}\)
\(=-\log_2 x\)
したがって、\(y=\log_{\frac{1}{2}} x\) のグラフは、
\(y=\log_2 x\) のグラフを \(x\) 軸に関して対称移動したもの。

(3) \(2x-4=2(x-2)\) より、積の大数の性質を利用して、右辺を分解します。
\(y=\log_2 (2x-4)=\log_2 2(x-2)\)
\(=\log_2 2+\log_2 (x-2)\)
\(=\log_2 (x-2)+1\)
したがって、\(y=\log_2 (2x-4)\) のグラフは、
\(y=\log_2 x\) のグラフを \(x\) 軸方向に \(2\)、\(y\) 軸方向に \(1\) だけ平行移動したもの。
例)\(A=(2\), \(1)\) が \(B=(4\), \(2)\)

対数関数のグラフまとめ
今回は、対数関数のグラフの性質やかき方についてでした。
関数問題は正しいグラフをかくことがとても重要です。最初は時間をかけてでも丁寧にかいていきましょう。
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている学生の方
- 公務員試験の数学で困っている学生/社会人の方
- 統計学(統計検定)の勉強で困っている学生/社会人の方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
時間や料金などは相談して決められればと思っておりますが、塾に通うよりは高コスパかなと思います。また、基本的にはオンラインでの授業を想定していますが、場所によっては直接の指導が可能です。(プロフィール)
これまでは塾講師や高校で働いていたのですが、現在はデータサイエンティストとして活動しています。社会やビジネスで数学がどのように使われているのか、そういった話も交えながら進められればと思っております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。





質問や感想はコメントへ!