接線の傾き \(=\) 微分係数
接線の方程式
\(y-f(a)=f'(a)(x-a)\)
法線の方程式
\(y-f(a)=-\displaystyle\frac{1}{f'(a)}(x-a)\) ただし \(f'(a)\neq 0\)
接線と法線
① 曲線 \(y=f(x)\) 上の接線と法線
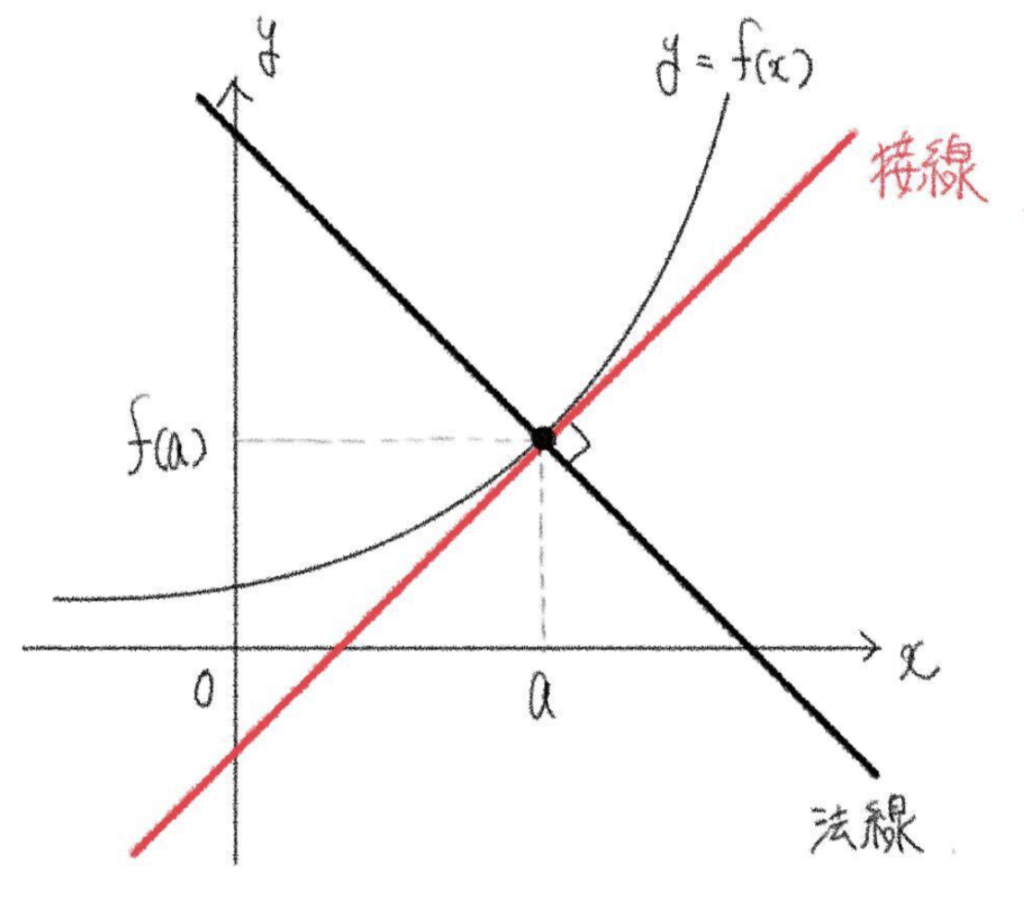
曲線 \(y=f(x)\) 上の点 \(A(a\), \(f(a))\) における
1 接線の方程式
\(y-f(a)=f'(a)(x-a)\)
2 法線の方程式
\(y-f(a)=-\displaystyle\frac{1}{f'(a)}(x-a)\)
ただし \(f'(a)\neq 0\)
② \(F(x\), \(y)=0\) や媒介変数で表される曲線の接線
曲線の方程式が、\(F(x\), \(y)=0\) や \(t\) を媒介変数として \(x=f(t)\), \(y=g(t)\) で表されるとき、曲線上の点 \((x_1\), \(y_1)\) における接線の方程式は \(y-y_1=m(x-x_1)\)
ただし、\(m\) は導関数 \(\displaystyle\frac{dy}{dx}\) に \(x=x_1\), \(y=y_1\) を代入して得られる値である。
（解説）
① 曲線 \(y=f(x)\) 上の接線と法線
曲線上の点 \(A\) を通り、\(A\) における接線に垂直な直線を、その曲線の点 \(A\) における法線という。曲線 \(y=f(x)\) 上の点 \(A(a\), \(f(a))\) における接線、法線の傾きはそれぞれ \(f'(a)\), \(-\displaystyle\frac{1}{f'(a)}\) [\(f'(a)\neq 0\)] であるから、\(A\) における接線、放線の方程式は上の 1, 2 のようになる。
② 曲線 \(F(x\), \(y)=0\) 上の接線
曲線 \(Ax^2+By^2=1\) \(\cdots\) ① 上の点 \((x_1\), \(y_1)\) における接線の方程式を求める。
① の両辺を \(x\) で微分すると
\(2Ax+2By\cdot y’=0\)
\(y_1\neq 0\) のとき
\(B\neq 0\) であるから、接線の傾き \(m\) は
\(y’=-\displaystyle\frac{Ax}{By}\) より \(m=-\displaystyle\frac{Ax_1}{By_1}\) ゆえに
\(y-y_1=-\displaystyle\frac{Ax_1}{By_1}(x-x_1)\)
よって
\(Ax_1x+By_1y=Ax_1^2+By_1^2\) また \(Ax_1^2+By_1^2=1\)
ゆえに、接線の方程式は
\(Ax_1x+By_1y=1\)
＜媒介変数表示 \(x=f(t)\), \(y=g(t)\) の曲線上の接線＞
\(x=a\cos\theta\), \(y=b\sin\theta\) (\(a>0\), \(b>0\)) で表される曲線上の \(\theta=\theta_1\) に対応する点における接線の方程式を求める。
\(\displaystyle\frac{dx}{d\theta}=-a\sin\theta\), \(\displaystyle\frac{dy}{d\theta}=b\cos\theta\) から
\(\displaystyle\frac{dy}{dx}=\frac{\displaystyle\frac{dy}{d\theta}}{\displaystyle\frac{dx}{d\theta}}=-\frac{b\cos\theta}{a\sin\theta}\)
接線と法線の問題
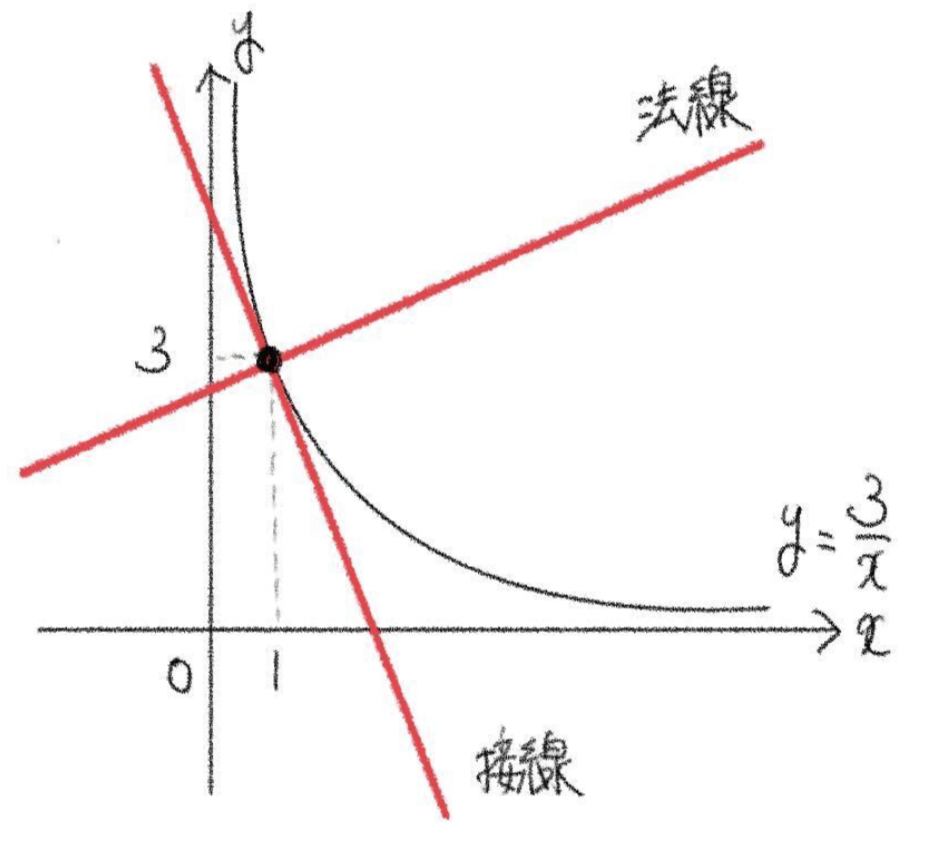
(1) 曲線 \(y=\displaystyle\frac{3}{x}\) 上の点 \((1\), \(3)\) における接線と法線の方程式を求めよ。
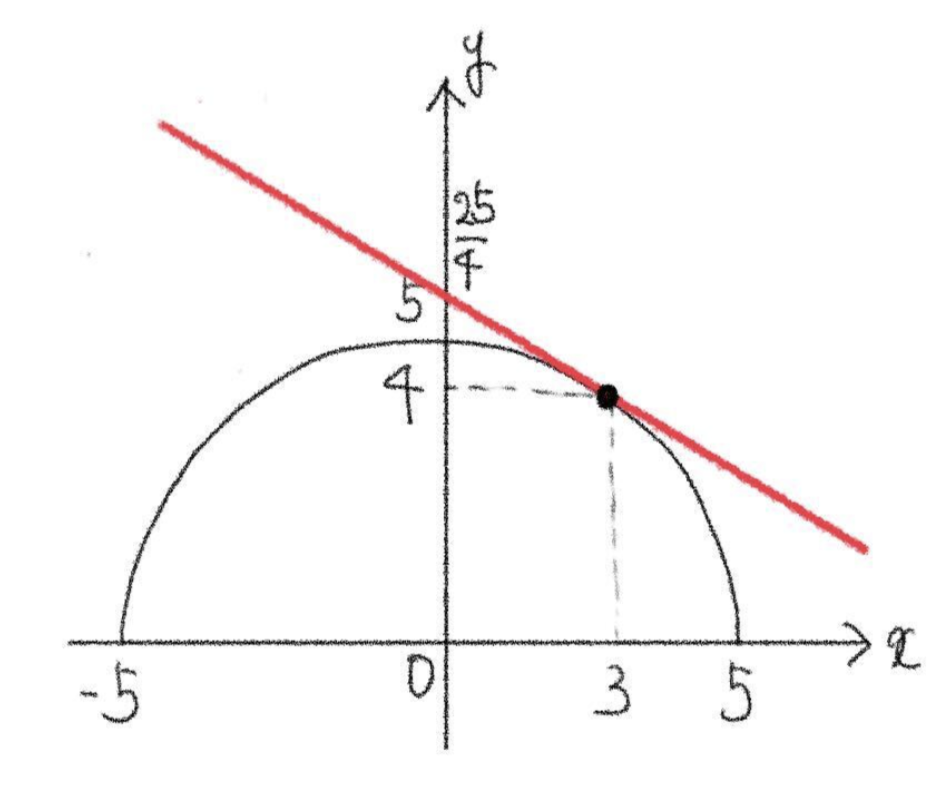
(2) 曲線 \(y=\sqrt{25-x^2}\) に接し、傾きが \(-\displaystyle\frac{3}{4}\) である直線の方程式を求めよ。
理系大学レベル別おすすめ数学テキスト
＞＞【理系大学向け】選ぶ時間を短縮！レベル別おすすめの数学参考書
解説
(1)
\(f(x)=\displaystyle\frac{3}{x}\) とすると、
\(f'(x)=3\cdot \big(-\displaystyle\frac{1}{x^2}\big)=-\frac{3}{x^2}\)
よって、
\(f'(1)=-\displaystyle\frac{3}{1^2}=-3\)
\(-\displaystyle\frac{1}{f'(1)}=\frac{1}{3}\)
接線の方程式は、
\(y-3=-3(x-1)\)
すなわち、
\(y=-3x+6\)
法線の方程式は、
\(y-30=\displaystyle\frac{1}{3}(x-1)\)
すなわち、
\(y=\displaystyle\frac{1}{3}x+\frac{8}{3}\)
(2)
\(f(x)=\sqrt{25-x^2}\) とすると
\(f'(x)=-\displaystyle\frac{x}{\sqrt{25-x^2}}\)
点 \((a\), \(f(a))\) における接線の方程式は、
\(y-\sqrt{25-a^2}=-\displaystyle\frac{a}{\sqrt{25-a^2}})(x-a)\) \(\cdots\) ①
この直線の傾きが \(-\displaystyle\frac{3}{4}\) であるとすると
\(-\displaystyle\frac{a}{\sqrt{25-a^2}}=-\frac{3}{4}\)
ゆえに \(4a=3\sqrt{25-a^2}\) \(\cdots\) ②
よって \(16a^2-9(25-a^2)\)
ゆえに \(a^2=9\)
②より \(a>0\) であるから \(a=3\)
\(a=3\) に代入して整理すると、
\(y=-\displaystyle\frac{3}{4}x+\frac{25}{4}\)
おわりに
さいごまで記事を読んでいただきありがとうございました！
数学は、時間をかけて勉強すれば誰でも成績を上げられます！
しかし、時間には限りがあります。
アプリや塾/家庭講師など自分に合ったサポートを取り入れることで、限りある時間を効率的に使うことができます。
▼自走して学習が進められる人
日々の悩みを解決できるコーチング面談や日々の学習計画を見直せるサポートがおすすめです。
▼自走して学習が進められない人
毎週講師による授業をしっかり受けて、宿題を設定してもらうサポートがおすすめです。
コメントはお気軽に♪