三角比で木の高さを求める
今回は、タンジェントを使って木の高さを測る問題を解説していきます。
タンジェントを使うことによって、下から木を眺めて高さを測ることができます。わざわざ登らなくても良いということですね！
↓三角比の定義はこちらをチェック！
木の高さをどうやって測る？
現代の便利なツールがないとしたら、実際にせっせと登って上からメジャーとかを垂らして測るのではないでしょうか？しかし、タンジェント（\(\tan\theta\)）という概念を知っていればわざわざ木登りで危険を冒してまで測る必要はありません。
高さ \(y\) を測るために必要な情報は、見上げた時の角度 \(\theta\) とその物との距離 \(x\) です。簡単に図にしてみるとこのようになります。
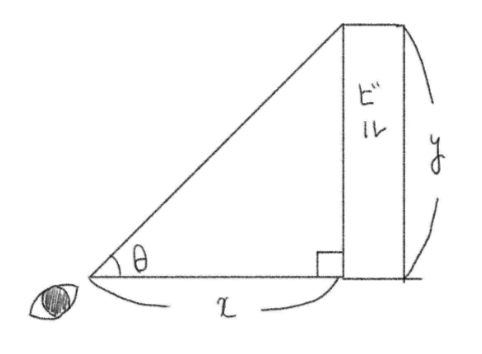
\(\tan\theta=\displaystyle\frac{y}{x}\) より
$$y=x\cdot\tan\theta$$
※図形問題のポイント
図形問題を解く際に、問題をただ眺めていても何をすれば良いのかは見えてきません。重要なことは、問題文から情報を抜き出し、図にしてみることです。そうすれば、何をすればいいのかが少しずつ見えてきます。
三角比で木の高さを求める（問題）
目の高さが \(1.5\) m の人が、平地に立っている木の高さを知るために、木の前方の地点 \(A\) から測った木の頂点の仰角が \(30^\circ\)、\(A\) から木に向かって \(10\) m 近づいた地点 \(B\) から測った仰角が \(45^\circ\) であった。木の高さを求めよ。
答案の例
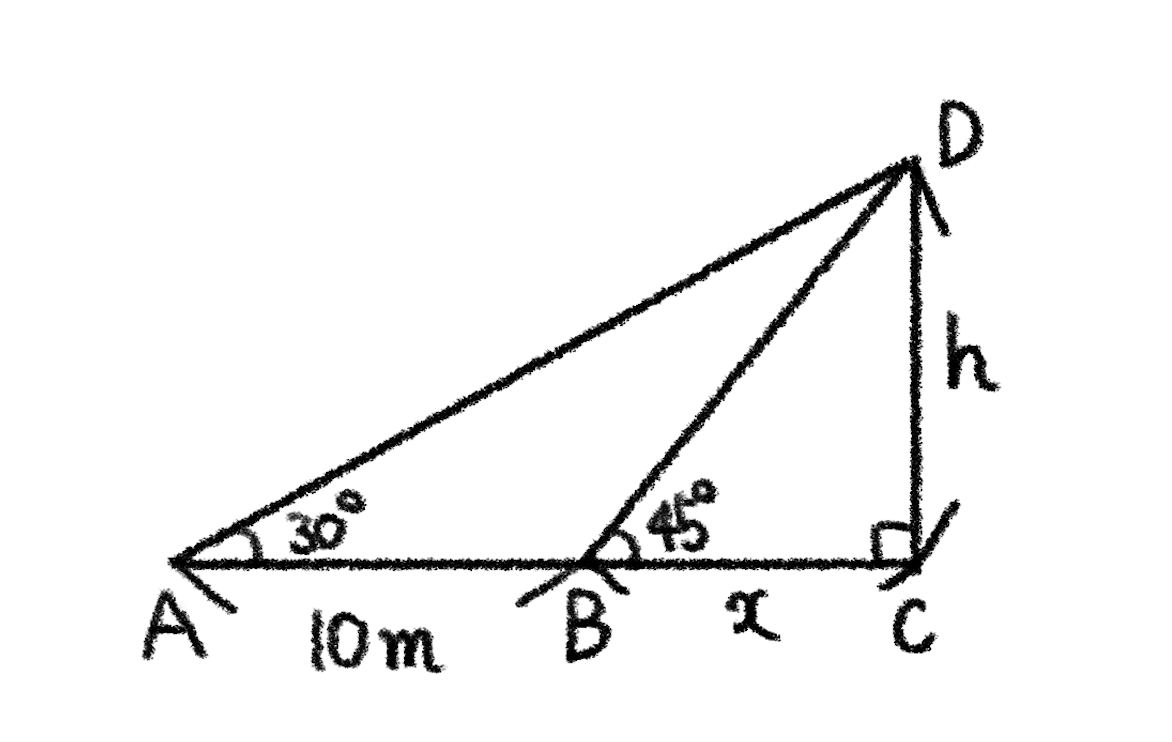
\(\triangle{ACD}\) において
$$\tan30^\circ=\displaystyle\frac{h}{10+x}$$
$$h=(10+x)\tan30^\circ$$
\(\tan30^\circ=\displaystyle\frac{1}{\sqrt{3}}\) より
$$h=\displaystyle\frac{10+x}{\sqrt{3}} \cdots ①$$
\(\triangle{BCD}\) において
$$\tan45^\circ=\displaystyle\frac{h}{x}$$
$$h=(x)\tan45^\circ$$
\(\tan45^\circ=1\) より
$$h=x \cdots ②$$
よって、
$$\begin{cases}h=\displaystyle\frac{10+x}{\sqrt{3}}\cdots ①\\h=x\cdots ②\end{cases}$$
①より
$$h=\displaystyle\frac{10+x}{\sqrt{3}}$$
$$h=\displaystyle\frac{10}{\sqrt{3}}+\frac{x}{\sqrt{3}}$$
②より
$$h=\displaystyle\frac{10}{\sqrt{3}}+\frac{h}{\sqrt{3}}$$
$$h-\displaystyle\frac{h}{\sqrt{3}}=\displaystyle\frac{10}{\sqrt{3}}$$
$$\left(1-\displaystyle\frac{1}{\sqrt{3}}\right)h=\displaystyle\frac{10}{\sqrt{3}}$$
$$\left(\displaystyle\frac{\sqrt{3}-1}{\sqrt{3}}\right)h=\displaystyle\frac{10}{\sqrt{3}}$$
\begin{eqnarray} h &=& \displaystyle\frac{10}{\sqrt{3}}\cdot\left(\displaystyle\frac{\sqrt{3}}{\sqrt{3}-1}\right)\\ &=& \displaystyle\frac{10}{\sqrt{3}-1}\\ &=& \displaystyle\frac{10\sqrt{3}+10}{2}=5\sqrt{3}+5 \end{eqnarray}木の高さを考慮すると、\(5\sqrt{3}+5+1.5=5\sqrt{3}+6.5\) (m)
解説
図を描くための情報を抜き出しましょう。
- 木の前方の地点 \(A\) から測った木の頂点の仰角が \(30^\circ\)
- \(A\) から木に向かって \(10\) m 近づいた地点 \(B\) から測った仰角が \(45^\circ\)
これらの情報を図に落とし込むと、
※ 目の高さの \(1.5\) m は図から省いています。
\(\triangle{ACD}\) において
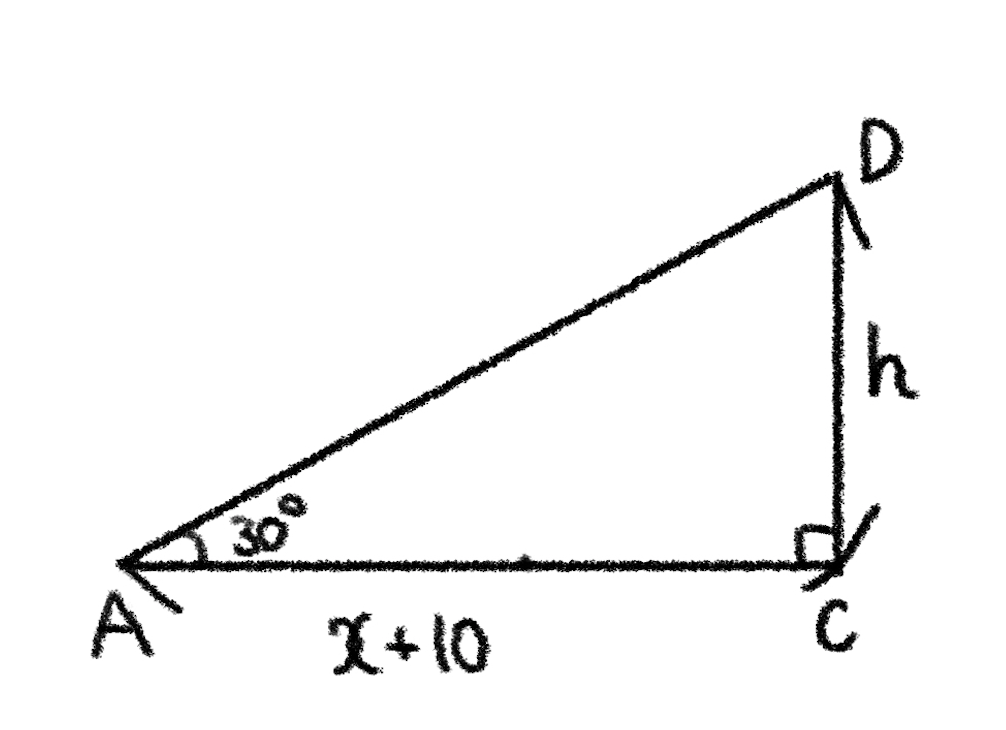
$$\tan30^\circ=\displaystyle\frac{h}{10+x}$$
$$h=(10+x)\tan30^\circ$$
\(\tan30^\circ=\displaystyle\frac{1}{\sqrt{3}}\) より
$$h=\displaystyle\frac{10+x}{\sqrt{3}} \cdots ①$$
\(\triangle{BCD}\) において
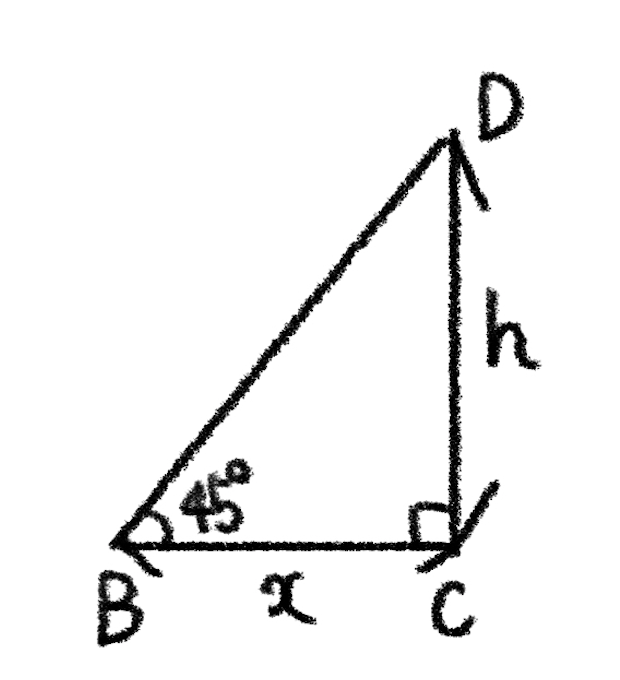
$$\tan45^\circ=\displaystyle\frac{h}{x}$$
$$h=(x)\tan45^\circ$$
\(\tan45^\circ=1\) より
$$h=x \cdots ②$$
$$\begin{cases}h=\displaystyle\frac{10+x}{\sqrt{3}}\\h=x\end{cases}$$
①より
$$h=\displaystyle\frac{10+x}{\sqrt{3}}$$
$$h=\displaystyle\frac{10}{\sqrt{3}}+\frac{x}{\sqrt{3}}$$
②より
$$h=\displaystyle\frac{10}{\sqrt{3}}+\frac{h}{\sqrt{3}}$$
整理すると、
$$h-\displaystyle\frac{h}{\sqrt{3}}=\displaystyle\frac{10}{\sqrt{3}}$$
$$\left(1-\displaystyle\frac{1}{\sqrt{3}}\right)h=\displaystyle\frac{10}{\sqrt{3}}$$
$$\left(\displaystyle\frac{\sqrt{3}-1}{\sqrt{3}}\right)h=\displaystyle\frac{10}{\sqrt{3}}$$
\begin{eqnarray} h &=& \displaystyle\frac{10}{\sqrt{3}}\cdot\left(\displaystyle\frac{\sqrt{3}}{\sqrt{3}-1}\right)\\ &=& \displaystyle\frac{10}{\sqrt{3}-1}\\ &=& \displaystyle\frac{10\sqrt{3}+10}{2}=5\sqrt{3}+5 \end{eqnarray}木の高さを考慮すると、\(5\sqrt{3}+5+1.5=5\sqrt{3}+6.5\) (m)
おわりに
今回は、タンジェントを使って木の高さを測る問題でした。
問題文を見て図にするのが難しかったかもしれません。
一度図にできれば、問題の糸口が見つけられるはずです。
さいごまで記事を読んでいただきありがとうございました！
「30分で集中力が切れてしまう方へ」
ポチップ
勉強の集中力UPのために
子供に集中して宿題をさせるために
会議やプレゼンのタイムマネジメントのために
質問や感想はコメントへ！
コメント一覧 （1件）
[…] 登らずして測る！タンジェントを使った木の高さの測り方 […]