円順列とじゅず順列の違い
今回は、円順列とじゅず順列について例題を交えながら解説していきます。
順列
異なる \(n\) 個のものの中から異なる \(r\) 個を選んで並べる。
その時の順列の総数は、\({}_nP_r=n\times (n-1)\times (n-2)\cdots (n-r+1)\)
円順列
いくつかのものを円形に並べる配列を円順列という。
円順列では、適当に回転して並びが一致するものは同じものとして考えるので、
\(\displaystyle\frac{{}_nP_n}{n}=(n-1)!\) となる。
じゅず順列
異なるいくつかのものを円形に並べ、回転または裏返して一致するものは同じものとみるとき、その並び方をじゅず順列という。
円順列の並び方の中には、裏返し一致するものが \(2\) つずつあり、
じゅず順列の総数は円順列の総数の半分なので、\(\displaystyle\frac{(n-1)!}{2}\) となる。
順列と円順列とじゅず順列の違い
順列と円順列
\(A\), \(B\), \(C\), \(D\) を 1 列に並べる順列を考える。
\(A\) \(B\) \(C\) \(D\)
\(B\) \(C\) \(D\) \(A\)
\(C\) \(D\) \(A\) \(B\)
\(D\) \(A\) \(B\) \(C\)
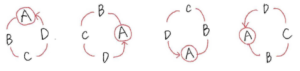
このように、\(1\) 列で並べると \(4\) 種類に分かれるものでも円状に並べてみると、同じ並び方になります。
※ 右回りもしくは左回りに回転させると同じ並び方になります。
順列と円順列
\(A\), \(B\), \(C\), \(D\) を 1 列に並べる順列を考える。
\(A\) \(B\) \(C\) \(D\)
\(B\) \(C\) \(D\) \(A\)
\(C\) \(D\) \(A\) \(B\)
\(D\) \(A\) \(B\) \(C\)
このように、\(1\) 列で並べると \(4\) 種類に分かれるものでも円状に並べてみると、同じ並び方になります。
※ 右回りもしくは左回りに回転させると同じ並び方になります。
円順列とじゅず順列の問題
異なる 6 個の宝石がある。
(1) これらの宝石を \(1\) 列に並べる方法は何通りあるか。
(2) これらの宝石を机の上で円形に並べる方法は何通りあるか。
(3) これらの宝石で首飾りを作るとき、何種類の首飾りができるか。
＞＞詳細はこちらから
円順列とじゅず順列（解説）
(1) これらの宝石を \(1\) 列に並べる方法は何通りあるか。
\(6!=6\times 5\times 4\times 3\times 2\times 1=720\)
(2) これらの宝石を机の上で円形に並べる方法は何通りあるか。
6 個の宝石を机の上で円形に並べる方法は、\(\displaystyle\frac{{}_6C_6}{6}=(6-1)!=5!=120\)
(3) これらの宝石で首飾りを作るとき、何種類の首飾りができるか。
(1) の並べ方のうち、裏返して一致するものを同じものと考えるので、\(\displaystyle\frac{(6-1)!}{2}=\frac{5!}{2}=60\)
おわりに
円順列
いくつかのものを円形に並べる配列を円順列という。
円順列では、適当に回転して並びが一致するものは同じものとして考えるので、
\(\displaystyle\frac{{}_nP_n}{n}=(n-1)!\) となる。
じゅず順列
異なるいくつかのものを円形に並べ、回転または裏返して一致するものは同じものとみるとき、その並び方をじゅず順列という。
円順列の並び方の中には、裏返し一致するものが \(2\) つずつあり、
じゅず順列の総数は円順列の総数の半分なので、\(\displaystyle\frac{(n-1)!}{2}\) となる。
それぞれ、問題文を見て使い分けを見極めましょう。
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！