\(a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\big(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\sin\theta+\frac{b}{\sqrt{a^2+b^2}}\cos\theta\big)\)
\(=\sqrt{a^2+b^2}\big(\sin\theta\cdot\displaystyle\frac{a}{\sqrt{a^2+b^2}}+\cos\theta\cdot\frac{b}{\sqrt{a^2+b^2}}\big)\)
\(=\sqrt{a^2+b^2}(\sin\theta\cos\alpha+\cos\theta\sin\alpha)\)
\(=\sqrt{a^2+b^2}\sin(\theta+\alpha)\)
三角関数の合成
\(a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)\) のように \(1\) つの三角関数にまとめることを合成といいます。（加法定理の逆の操作です。）
① 加法定理の逆の操作で計算する
② 図をかいて計算する
加法定理の逆の操作
\(a\sin\theta+b\cos\theta\)
\(=\sqrt{a^2+b^2}\) \(\big(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\sin\theta+\frac{b}{\sqrt{a^2+b^2}}\cos\theta\big)\)
\(=\sqrt{a^2+b^2}\big(\sin\theta\cdot\displaystyle\frac{a}{\sqrt{a^2+b^2}}+\cos\theta\cdot\frac{b}{\sqrt{a^2+b^2}}\big)\)
\(=\sqrt{a^2+b^2}\big(\sin\theta\cdot\displaystyle\frac{a}{\sqrt{a^2+b^2}}+\cos\theta\cdot\frac{b}{\sqrt{a^2+b^2}}\big)\)
\(=\sqrt{a^2+b^2}(\sin\theta\cos\alpha+\cos\theta\sin\alpha)\)
\(=\sqrt{a^2+b^2}\sin(\theta+\alpha)\)
（手順）
\(2\) 行目：\(\sqrt{a^2+b^2}\) で強引に括っていますが、必ず \(2\) 乗の和が \(1\) となる分数 \(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\) と \(\displaystyle\frac{b}{\sqrt{a^2+b^2}}\) が出てきます。
\(3\) 行目：並び替え
\(4\) 行目：\(\displaystyle\frac{a}{\sqrt{a^2+b^2}}=\cos\alpha\), \(\displaystyle\frac{b}{\sqrt{a^2+b^2}}=\sin\alpha\) とできるような偏角 \(\alpha\) を探して変形
\(5\) 行目：加法定理の逆の操作で \(\sin\) でまとめます。
\(\cos\) への合成
\(a\sin\theta+b\cos\theta\)
\(=\sqrt{a^2+b^2}\big(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\sin\theta+\frac{b}{\sqrt{a^2+b^2}}\cos\theta\big)\)
\(=\sqrt{a^2+b^2}\big(\cos\theta\cdot\displaystyle\frac{b}{\sqrt{a^2+b^2}}+\sin\theta\cdot\frac{a}{\sqrt{a^2+b^2}}\big)\)
\(=\sqrt{a^2+b^2}(\cos\theta\cos\alpha+\sin\theta\sin\alpha)\)
\(=\sqrt{a^2+b^2}\cos(\theta-\alpha)\)
図をかいて計算する
この方法は、\(\sin\) の合成限定の方法です。図にすると応用がききますが、上の内容が十分に理解できていないと難しいかもしれません。難しいと感じる人はまずは上の方法でこの後の練習問題を解いてみてください。
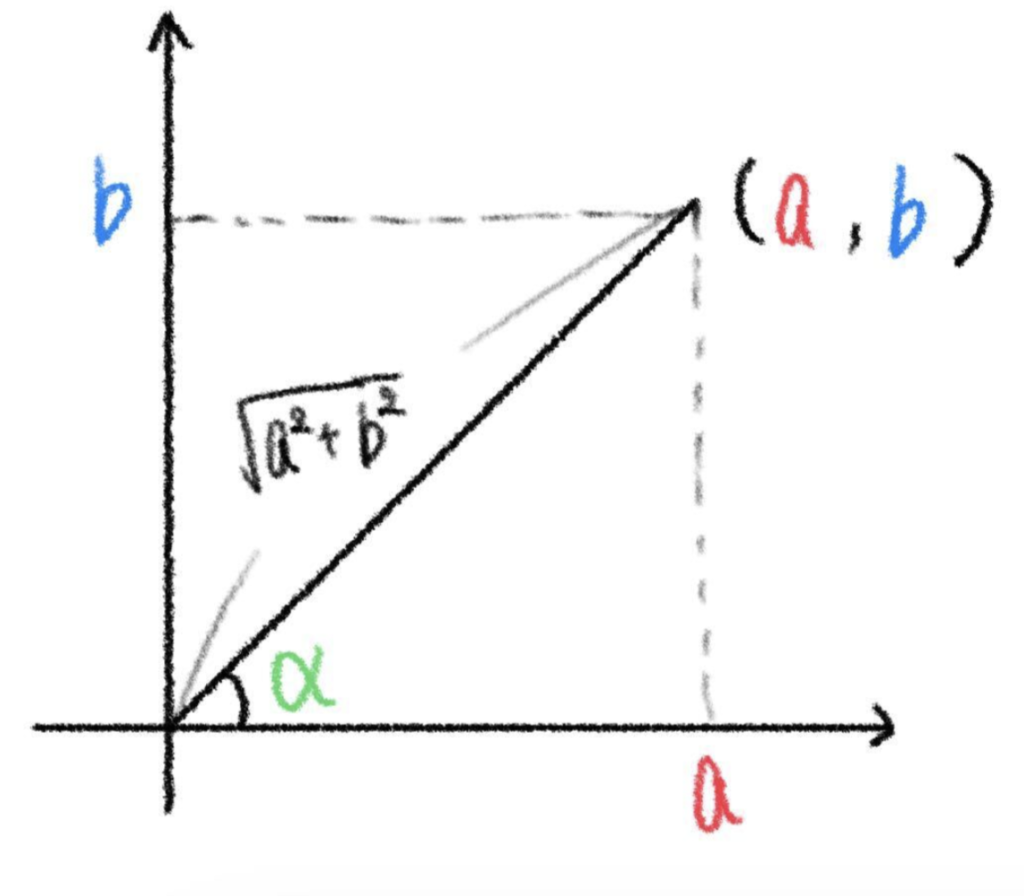
\(a\) \(\sin\theta+\) \(b\) \(\cos\theta\)
\(=\sqrt{a^2+b^2}\cos\alpha\) \(\sin\theta+\) \(\sqrt{a^2+b^2}\sin\alpha\) \(\cos\theta\)
\(=\sqrt{a^2+b^2}(\sin\theta\cos\alpha+\cos\theta\sin\alpha)\)
\(=\sqrt{a^2+b^2}\sin(\theta+\alpha)\)
\(\alpha\) は座標平面上の点 \((a\), \(b)\) と原点とのなす角
理系大学レベル別おすすめ数学テキスト
＞＞【理系大学向け】選ぶ時間を短縮！レベル別おすすめの数学参考書
三角関数の合成の基本問題
次の式を、\(r\sin(\theta+\alpha)\) の形に変形せよ。ただし、 \(r>0\), \(-\pi<\alpha<\pi\)
(1) \(\sqrt{3}\sin\theta+\cos\theta\)
(2) \(\sin\theta-\cos\theta\)
（解説）
\(\sqrt{a^2+b^2}\) で強引に括るのが第一歩
(1) \(\sqrt{3}\sin\theta+\cos\theta\)
\(=\sqrt{\sqrt{3}^2+1^2}\big(\displaystyle\frac{\sqrt{3}}{2}\sin\theta+\frac{1}{2}\cos\theta\big)\)
\(=2\big(\sin\theta\cdot\displaystyle\frac{\sqrt{3}}{2}+\cos\theta\cdot\frac{1}{2}\big)\)
\(\cos\alpha=\displaystyle\frac{\sqrt{3}}{2}\), \(\sin\alpha=\displaystyle\frac{1}{2}\) となるような \(\alpha\) を探す。
\(=2\big(\sin\theta\cos\displaystyle\frac{\pi}{6}+\cos\theta\sin\frac{\pi}{6}\big)\)
\(=2\sin\big(\theta+\displaystyle\frac{\pi}{6}\big)\)
（別解）
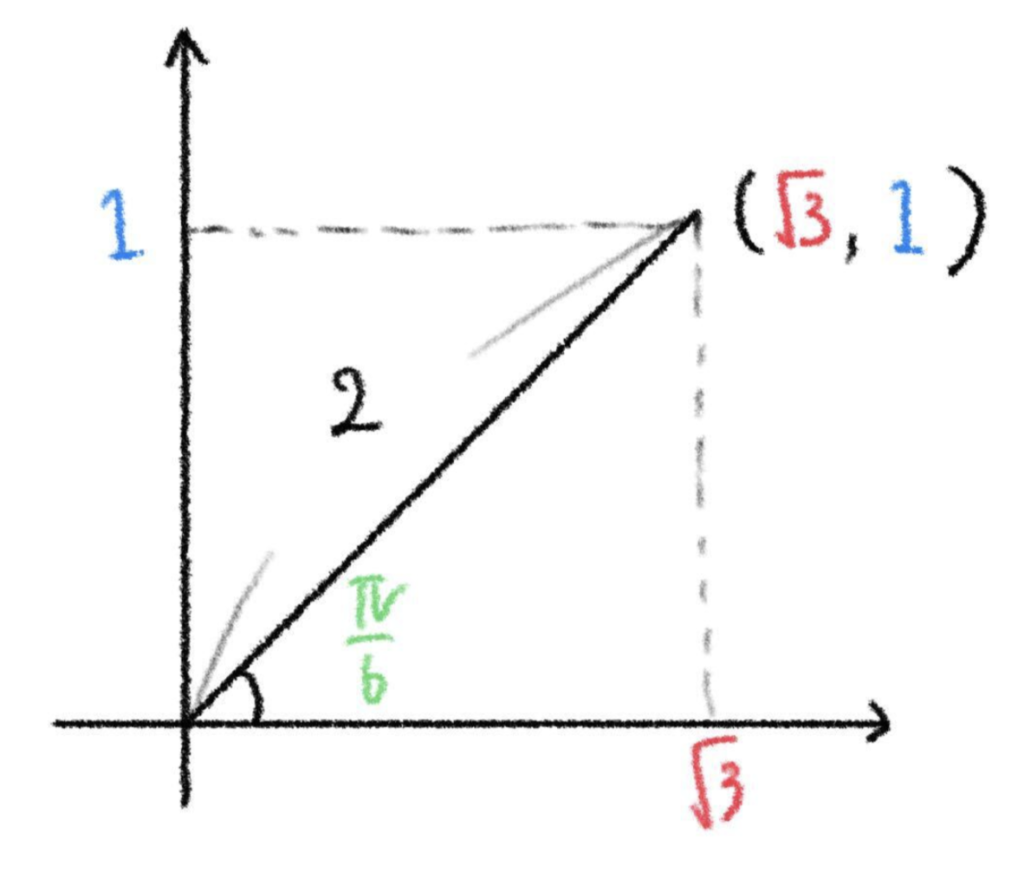
\(\sqrt{3}\) \(\sin\theta+\) \(1\) \(\cos\theta\)
\(=2\sin\big(\theta+\displaystyle\frac{\pi}{6}\big)\)
(2) \(\sin\theta-\cos\theta\)
\(=\sqrt{1^2+1^2}\big(\displaystyle\frac{1}{\sqrt{2}}\sin\theta-\frac{1}{\sqrt{2}}\cos\theta\big)\)
\(=\sqrt{2}\big(\sin\theta\cdot\displaystyle\frac{1}{\sqrt{2}}-\cos\theta\cdot\frac{1}{\sqrt{2}}\big)\)
\(\cos\alpha=\displaystyle\frac{1}{\sqrt{2}}\), \(\sin\alpha=\displaystyle\frac{1}{\sqrt{2}}\) となるような \(\alpha\) を探す。
\(=\sqrt{2}\big(\sin\theta\cos\displaystyle\frac{\pi}{4}-\cos\theta\sin\frac{\pi}{4}\big)\)
\(=\sqrt{2}\sin\big(\theta-\displaystyle\frac{\pi}{4}\big)\)
（別解）
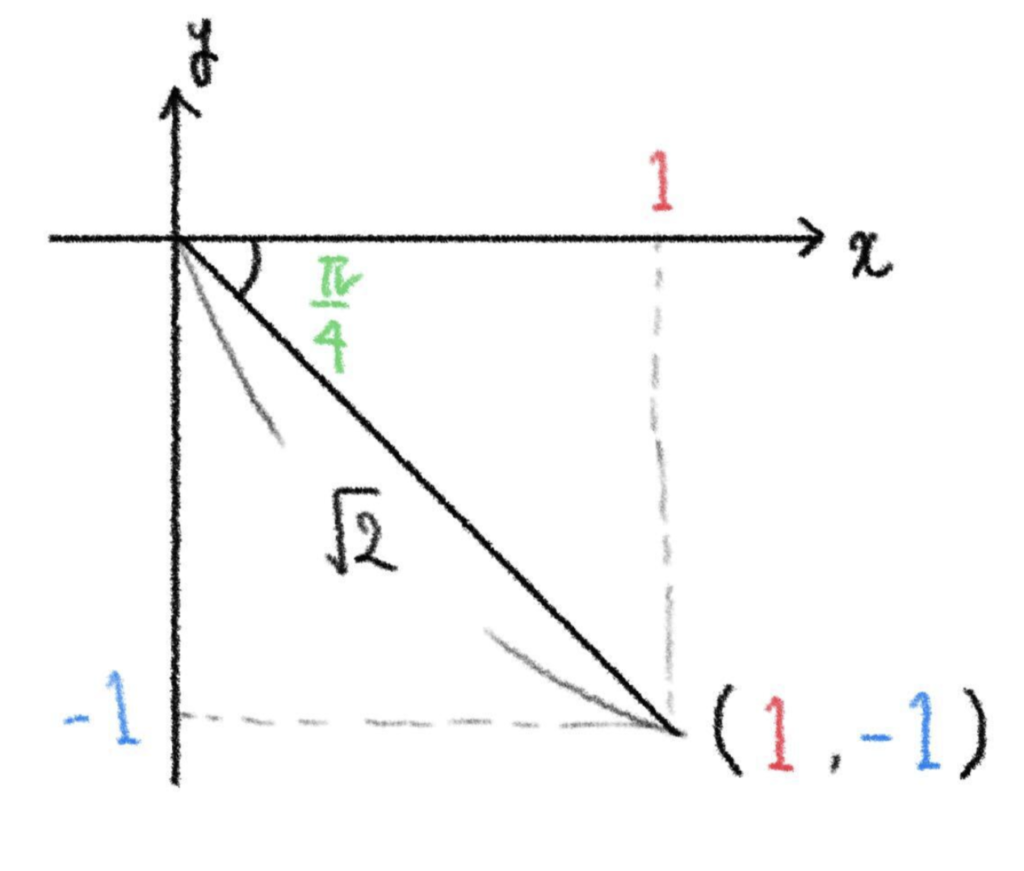
\(1\) \(\sin\theta+\) \((-1)\) \(\cos\theta\)
\(=\sqrt{2}\sin\big\{\theta+\big(-\displaystyle\frac{\pi}{4}\big)\big\}\)
\(=\sqrt{2}\sin\big(\theta-\displaystyle\frac{\pi}{4}\big)\)
三角関数の合成の応用問題
\(y=3\cos x+4\sin x\) \((0\leq x \leq \pi)\) の最大値、最小値を求めよ。
（解説）
\(y=3\cos x+4\sin x\)
\(=\sqrt{3^2+4^2}\big(\displaystyle\frac{3}{5}\cos x+\frac{4}{5}\sin x\big)\)
\(\cos\alpha=\displaystyle\frac{3}{5}\), \(\sin\alpha=\displaystyle\frac{4}{5}\) を満たす \(\alpha\) は、存在はするが簡単には見つけられないため \(\alpha\) のままで計算を進める。ただし、\(0\leq \alpha \leq \frac{\pi}{2}\)
\(=5\cos(x-\alpha)\)
\(-\alpha\leq x-\alpha\leq\pi-\alpha\) また、\(-\frac{\pi}{2}< -\alpha<0\), \(\frac{\pi}{2}<\pi-\alpha<\pi\) より
\(x=\alpha\) のとき、最大値 \(5\)
\(x=\pi\) のとき、最小値 \(-3\)
おわりに
さいごまで記事を読んでいただきありがとうございました！
数学は、時間をかけて勉強すれば誰でも成績を上げられます！
しかし、時間には限りがあります。
アプリや塾/家庭講師など自分に合ったサポートを取り入れることで、限りある時間を効率的に使うことができます。
▼自走して学習が進められる人
日々の悩みを解決できるコーチング面談や日々の学習計画を見直せるサポートがおすすめです。
▼自走して学習が進められない人
毎週講師による授業をしっかり受けて、宿題を設定してもらうサポートがおすすめです。
コメントはお気軽に♪