この記事では「正弦定理と余弦定理の証明」について解説します!
正弦定理/余弦定理の証明
正弦定理と余弦定理は高校数学では非常に重要な公式です。試験中のど忘れを防ぐためにも導出を知っておきましょう。
また、入試で公式の証明問題が出題されることもありますので、この記事を通して導き方を確認しましょう!
正弦定理の公式
正弦定理
三角形 \(\triangle{ABC}\) の外接円の半径を \(R\) としたとき、
\(\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)
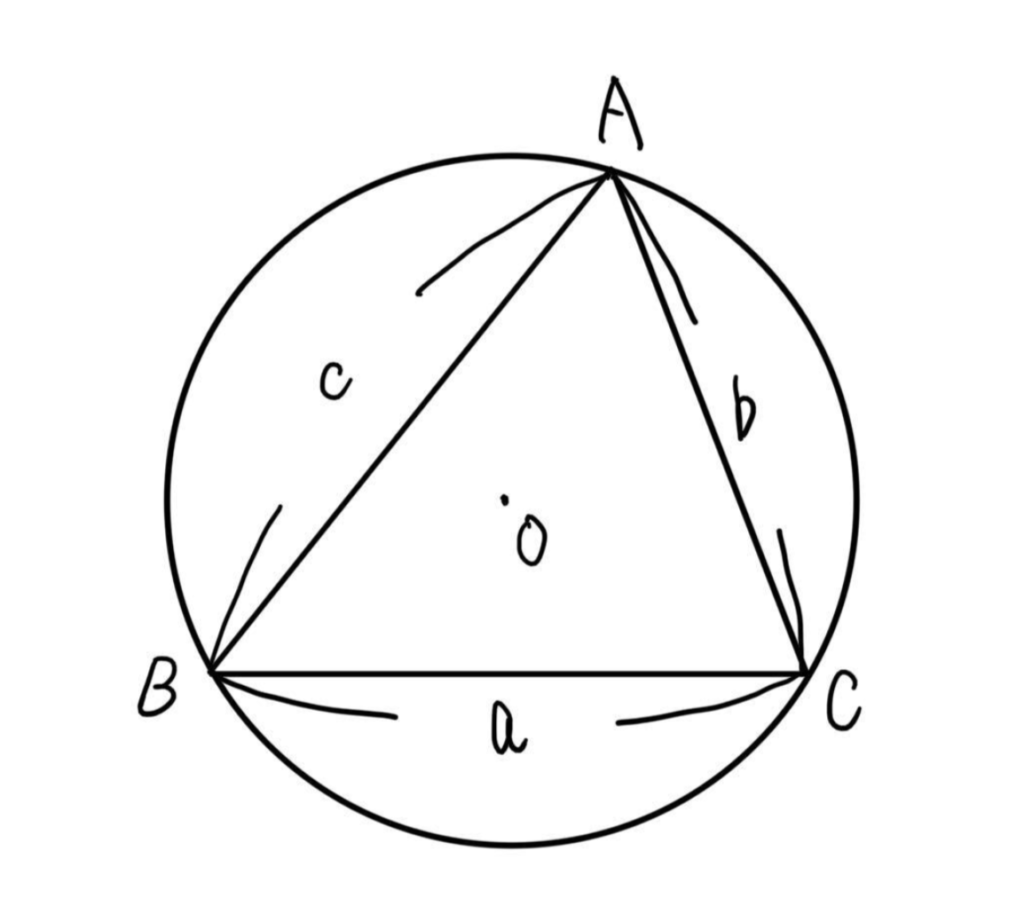
正弦定理の証明
\(\displaystyle\frac{a}{\sin A}=2R\) について証明します。
※ \(\angle{B}\), \(\angle{C}\) についても同様のやり方で証明できます。
- \(\angle{A}\) が鋭角のとき
- \(\angle{A}\) が直角のとき
- \(\angle{A}\) が鈍角のとき
これら \(3\) つの場合をすべて証明すれば、「\(\angle{A}\) がどんなときでも正弦定理は成り立つ」ことになります。
※ このように、証明は「常に」、「どんな場合でも」成り立つことを示す必要があります。
\(\angle{A}\) が鋭角のとき

右側の図で、
\(\sin A’=\displaystyle\frac{a}{2R}\)
また、円周角の定理より \(\angle{A}=\angle{A’}\) なので、
\(\displaystyle\frac{a}{\sin A}=2R\)
\(\angle{A}\) が直角のとき
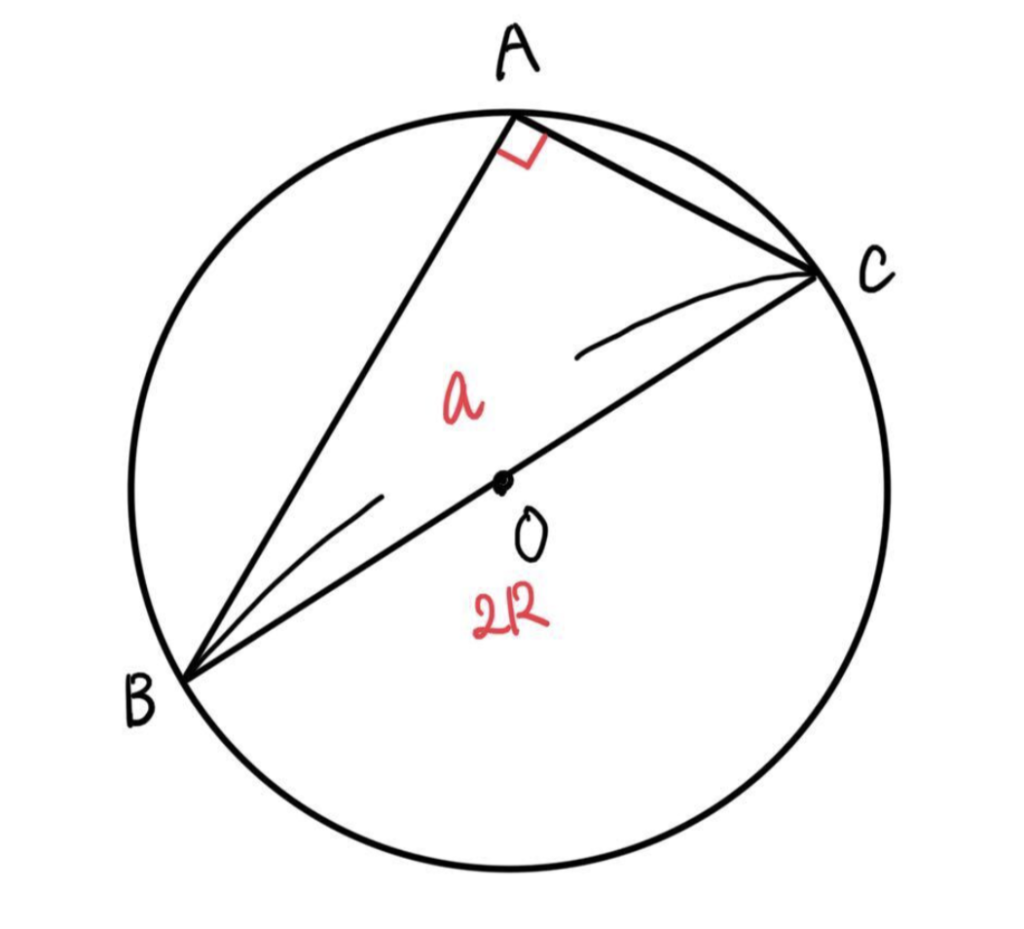
\(\angle{A}=90^{\circ}\) のとき、上の図より
\(a=2R\)
よって、
\(\displaystyle\frac{a}{2R}=1\)
となります。また、\(\sin90^{\circ}=1\) なので、
\(\displaystyle\frac{a}{2R}=\sin90^{\circ}\)
したがって、
\(\displaystyle\frac{a}{\sin90^{\circ}}=2R\)
\(\angle{A}\) が鈍角のとき
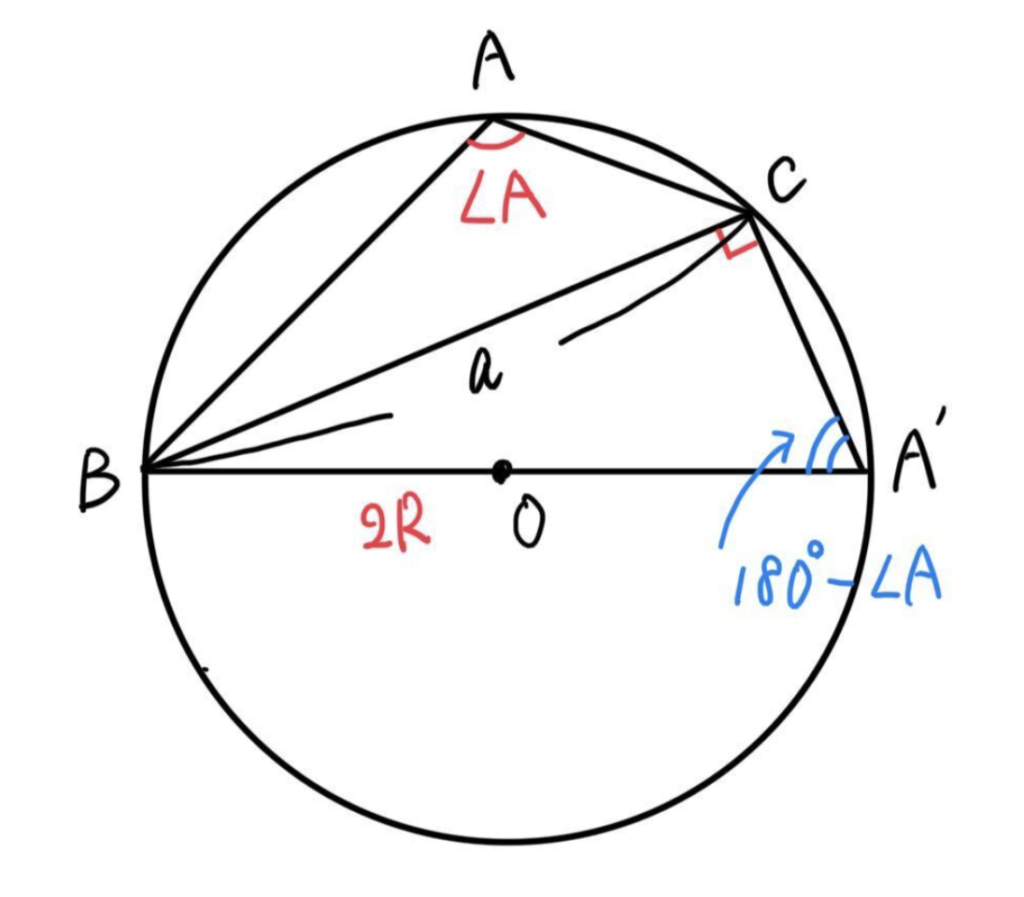
四角形 \(ABA’C\) は円に内接しているので、内接四角形の性質より、
\(\angle{A}+\angle{A’}=180^{\circ}\)
\(\angle{A’}=180^{\circ}-\angle{A}\)
よって、\(\sin A’=\sin(180^{\circ}-A)\)
\(180^{\circ}-\theta\) の変換公式より、
\(\sin (180^{\circ}-A)=\sin A\)
したがって、\(\sin A’=\sin A\) \(\cdots\) ①
また、\(\triangle{A’BC}\) に着目すると
\(\sin A’=\displaystyle\frac{a}{2R}\)
\(\displaystyle\frac{a}{\sin A’}=2R\) \(\cdots\) ②
①, ② より
\(\displaystyle\frac{a}{\sin A}=2R\)
以上より、
\(\displaystyle\frac{a}{\sin A}=2R\)
が示せました。
\(\angle{B}\), \(\angle{C}\) についても同様に証明することで、正弦定理
\(\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)
余弦定理の公式
余弦定理
\(a^2=b^2+c^2-2bc\cos A\)
\(b^2=c^2+a^2-2ca\cos B\)
\(c^2=a^2+b^2-2ab\cos C\)
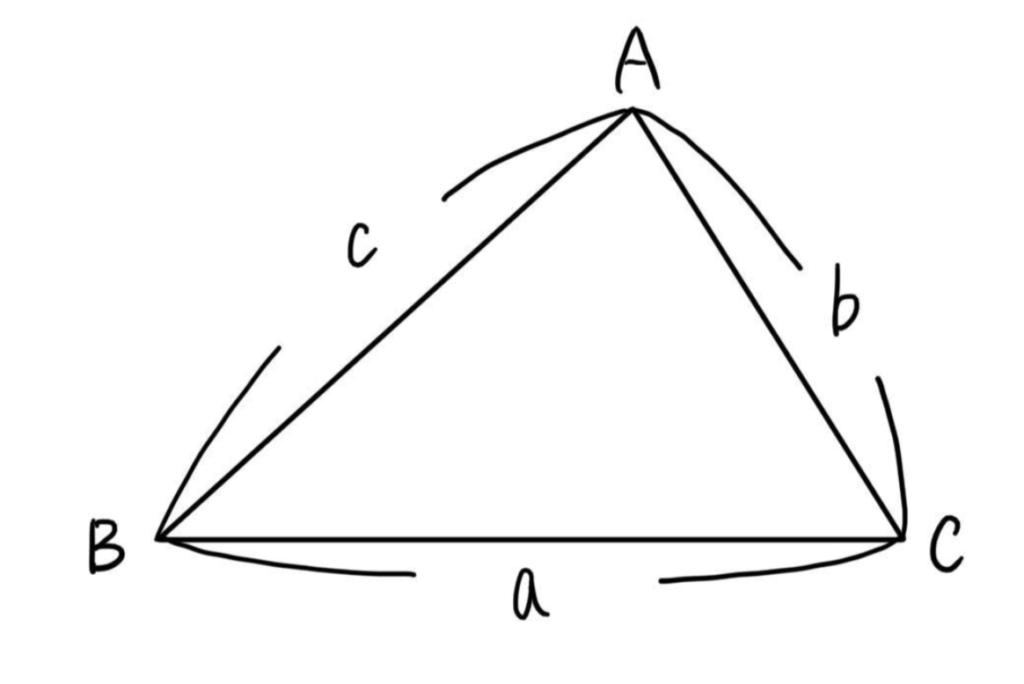
余弦定理の証明
正弦定理と同様に
- \(\angle{A}\) が鋭角のとき
- \(\angle{A}\) が直角のとき
- \(\angle{A}\) が鈍角のとき
の \(3\) つの場合に分けて証明します。
\(\angle{A}\) が鋭角のとき
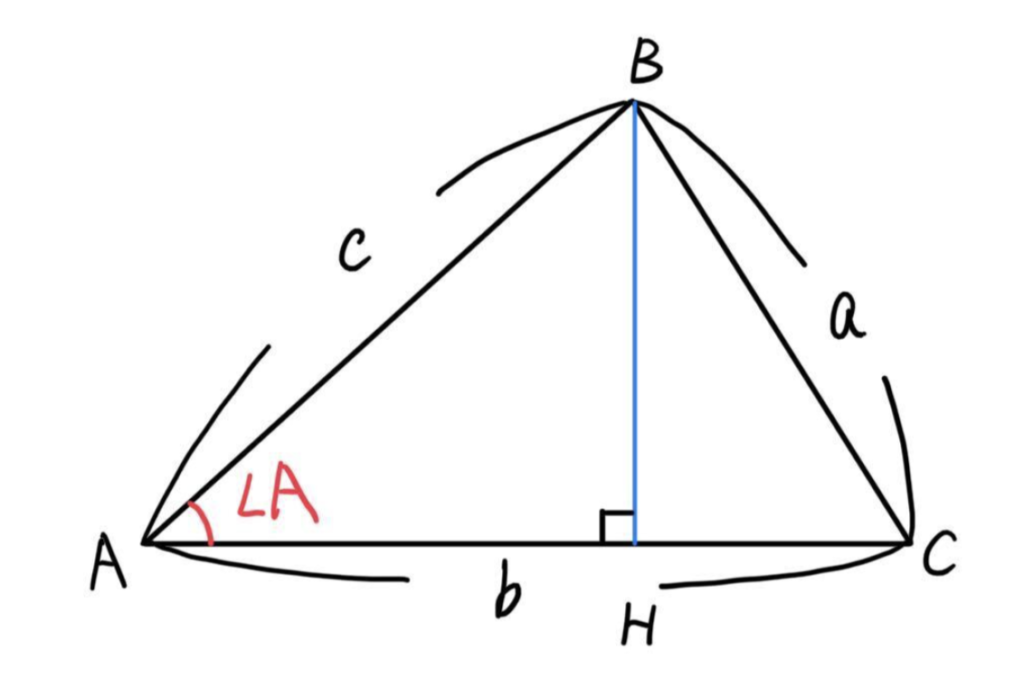
\(\triangle{ABH}\) に着目すると
\(AH=c\cdot\cos A\), \(BH=c\cdot\sin A\)
次に、\(\triangle{BCH}\) で三平方の定理を適用すると、
\(BC^2=BH^2+CH^2\)
\(a^2=(c\cdot\sin A)^2+(b-c\cdot\cos A)^2\)
\(=c^2\sin^2 A+b^2-2bc\cdot\cos A+c^2\cos^2 A\)
\(=c^2(\sin^2 A+\cos^2 A)+b^2-2bc\cdot\cos A\)
\(=c^2\cdot 1+b^2-2bc\cdot\cos A\)
\(=c^2+b^2-2bc\cdot\cos A\)
\(\angle{A}\) が直角のとき

\(\angle{A}=90^{\circ}\) のとき、「余弦定理は三平方の定理そのもの」といえます。
上の図で、三平方の定理より、
\(a^2=b^2+c^2\)
であり、\(\cos A=\cos 90^{\circ}=0\) なので、
\(a^2=b^2+c^2-2bc\cos A\)
が成り立っています(\(\cos A=0\) だから)。
\(\angle{A}\) が鈍角のとき
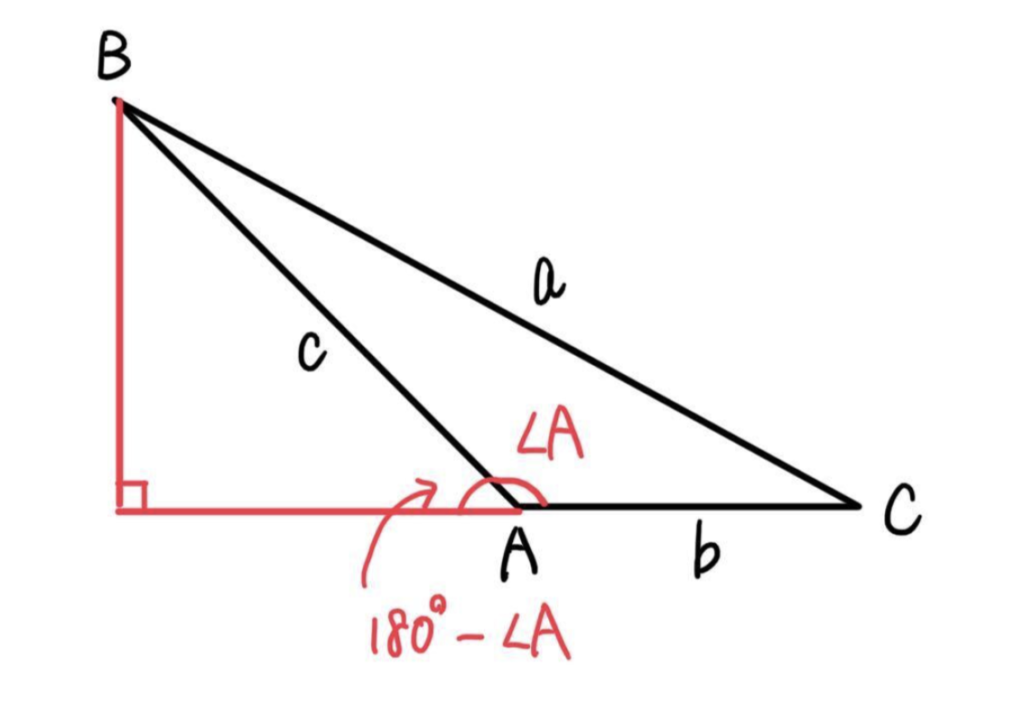
\(BH=c\cdot\sin(180^{\circ}-A)=c \sin A\)
\(AH=c\cdot\cos(180^{\circ}-A)=-c \cos A\)
次に、\(\triangle{BCH}\) で三平方の定理を適用すると、
\(BC^2=BH^2+CH^2\)
\(=BH^2+(AC+AH)^2\)
\(a^2=(c\sin A)^2+(b-c\cos A)^2\)
\(=c^2\sin^2 A+b^2-2bc\cdot \cos A+c^2\cos^2 A\)
\(=c^2(\sin^2 A+\cos^2 A)+b^2-2bc\cdot \cos A\)
\(=c^2\cdot 1+b^2-2bc\cdot \cos A\)
\(a^2=c^2+b^2-2bc\cdot \cos A\)
以上より、
\(a^2=b^2+c^2-2bc\cos A\)
が示めせました。
他の \(2\) つの式についても、同様に証明することができます。
おわりに
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている学生の方
- 公務員試験の数学で困っている学生/社会人の方
- 統計学(統計検定)の勉強で困っている学生/社会人の方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
時間や料金などは相談して決められればと思っておりますが、塾に通うよりは高コスパかなと思います。また、基本的にはオンラインでの授業を想定していますが、場所によっては直接の指導が可能です。(プロフィール)
これまでは塾講師や高校で働いていたのですが、現在はデータサイエンティストとして活動しています。社会やビジネスで数学がどのように使われているのか、そういった話も交えながら進められればと思っております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。




質問や感想はコメントへ!